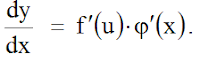Forţa - definiţie şi caracteristici

Autor: ing. Constantin Teodorescu

Articolul "Forţa - definiţie şi caracteristici" reia ultima parte a capitolului "13 Mişcarea. Legi, principii şi caracteristici" din studiul "Structură şi evoluţie", în care se demonstrează că forţa este gradientul energiei în mişcare şi se prezintă şi principalele caracteristici ale acesteia.

Cuprins:
1  Definiţia forţei
2  Forţe naturale şi forţe create

1  Definiţia forţei

În finalul subparagrafului precedent, s-a vorbit despre forţe de bază şi forţe provenite sau derivate, care mai pot fi numite şi forţe obiective şi, respectiv, subiective, şi considerăm că se cuvin câteva lămuriri suplimentare. Mai întâi însă trebuie definită noţiunea de forţă.

Cuvântul forţă este folosit în vorbirea curentă, în înţelesul de obligaţie de a executa o anumită acţiune. De exemplu, „am fost forţat să execut această acţiune” sau „în caz de forţă majoră”. În fizică însă, cuvântul forţă semnifică un vector care acţionează pe o anumită direcţie şi într-un anumit sens. Iar din punctul de vedere al concepţiei elaborate în prezentul studiu, noţiunea de forţă, fiind una dintre noţiunile fundamentale, necesită o definiţie cât mai clară şi precisă.

În subcapitolul 2.2 din [1], în subparagraful 2.2.2.1, prin relaţia (2.2.7), care este reluată ca relaţia (1), s-a demonstrat că forţa centrifugă a mişcării giroscopice este gradientul energiei giroscopice:

          (1)

Tot în [1], subcapitolul 2.2, paragreful 2.2.3, prin relaţia (2.2.31), reluată ca relaţia (2),

           (2)

s-a demonstrat că forţa centrifugă deplasează energia giroscopică de-a lungul razei de rotaţie, prefigurând expresia legii fundamentale a mişcării demonstrată în subparagraful 9.4.1, relaţia (9.33), tot din [1]. (A se vedea şi postarea „Legeafundamentală a mişcării” tot pe blogul acesta).

Pe baza relaţiei (2.2.31), în capitolul 5 din [1], considerând că elementul e de energie, care se roteşte în cadrul unei structuri de energie cu mişcare giroscopică, este împins de-a lungul razei tot de forţa centrifugă, pe de o parte, iar forţa centrifugă este gradientul energiei giroscopice, pe de altă parte, s-a determinat expresia energiei giroscopice a elementului de energie prin relaţia (5.31), care este reluată ca relaţia (3),

             (3)

ca funcţia polară a unghiului polar.

Prin determinarea potenţialului vectorial al gradientului energiei giroscopice, în paragraful 5.5 din [1], s-a dovedit că expresia (3) este valabilă doar în planul ecuatorial al structurii de energie cu mişcare giroscopică, pentru z = 0, iar pentru z diferit de 0, energia giroscopică se exprimă prin relaţia (5.64), care este preluată ca relaţia (4), adică

               (4)

în care expresia e(z + 1) reprezintă energia giroscopică a cărei densitate creşte cu depărtarea de planul ecuatorial (z = 0).

Pe baza acestor argumente, există tentaţia firească de a defini forţa prin gradientul energiei pe care o deplasează.Ca să vedem însă dacă definiţia este corectă, trebuie să verificăm dacă este şi general valabilă.

Ca o primă verificare, să determinăm gradientul energiei giroscopice exprimată prin  relaţia (4). În acest scop, mai întâi, să exprimăm relaţia, în coordonate carteziene:

        (5)

Apoi, conform relaţiei (2.2.5) din [1], pentru aflarea gradientului, trebuie determinate derivatele parţiale pe cele trei coordonate x, y, z, care constituie componentele sale.

Conform [2], din tabelul derivatelor principalelor funcţii de lapag. 307, scoatem formula derivatei unghiului arctg,

          (6)

iar de la pag. 309 pct. 5), luăm formula de derivare a funcţiei complexe y = f(u) şi u = v(x):

           (7)

Calculul derivatelor parţiale ale energiei giroscopice exprimată prin relaţia (5), pe  coordonatele x, y, z, pe baza relaţiilor (6) şi (7), conduce la expresiile:

      (8)

      (9)

     (10)

Cu componentele date de expresiile (8), (9) şi (10), vectorul gradient al energiei giroscopice dintr-o structură de energie are forma

    (11)

Vectorial, relaţia (11) este identică cu relaţia (5.32) din capitolul 5 din [1] şi reprezintă un vector paralel cu planul ecuatorial, perpendicular pe forţa centrifugă şi tangent la traiectoria circulară pe care se roteşte energia giroscopică, în jurul axei de rotaţie a structurii de energie cu mişcare giroscopică.

Având aceeaşi mărime (modul) cu vectorul forţei centrifuge, gradientul energiei giroscopice reprezintă forţa care roteşte energia giroscopică pe traiectoria circulară, în jurul axei de rotaţie, în sensul invers acelor de ceasornic.

Astfel, ca vector de forţă, gradientul energiei giroscopice a structurii de energie cu mişcare giroscopicăconfirmă concluziile din paragraful 2.2.3 din subcapitolul 2.2 din [1] şi confirmă şi satisface şi condiţiile legii fundamentale a mişcării, prezentate în paragraful 13.4.1 din [1]. (A se vedea şi postarea „Legea fundamentală a mişcării” pe acest blog).

Existenţa termenului e k în relaţia (11), care nu are semnificaţie vectorială, arată caracterul cumulativ al gradientului energiei giroscopice, aspect normal şi firesc deoarece este în concordanţă cu caracterul cumulativ şi al energiei giroscopice. De asemenea, termenul ek arată că aspectul cumulativ se manifestă, la gradientul energiei giroscopice, nu spaţial ci ca intensitate, dar în deplină concordanţă cu manifestarea aspectului cumulativ la energia giroscopică.

Totodată, gradientul energiei giroscopice relevă şi deosebirea fundamentală dintre mişcarea giroscopică a corpului material şi mişcarea giroscopică a structurii de energie.

Corpul material, având o structură fixă şi stabilă, cu masa uniform distribuită în tot volumul ocupat, cum s-a presupus în subcapitolul 2.2 din [1], forţa centrifugă a acestuia împinge energia radial, iar rotirea energiei, simultană cu rotirea masei, este realizată de o forţă exterioară, egală cu forţa centrifugă, şi se menţine şi după încetarea forţei exterioare, pe seama acumulării de energie, din câmpul de energie ce înconjoară corpul material, realizată prin caracterul cumulativ al structurii de energie formată de energia giroscopică a elementelor corpului material, peste întregul corp material. Când acumularea de energie devine mai mică decât energia consumată pentru rotire, mişcarea de rotaţie diminuează treptat şi încetează.

Spre deosebire de corpul material, structura de energie cu mişcare giroscopică, prin gradientul energiei giroscopice, îşi crează propria forţă de rotire a energiei care, pe baza caracterului său cumulativ, se întreţine prin asimilarea de energie din câmpul exterior structurii, aşa cum s-a demonstrat în capitolul 5 din [1]şi cum a fost preluat, în formă concentrată, în paragraful 13.3 tot din [1]. (A se vedea şi postarea „Mișcarea de rotație” tot pe acest blog).

Prin urmare, se poate reţine următoarea concluzie:

a)      În mişcarea de rotaţie, atât a corpurilor materiale cât şi a structurilor de energie, forţa de rotaţie reprezintă gradientul energiei giroscopice. 

Pentru a generaliza această definiţie a forţei, este necesară însă verificarea valabilităţii şi pentru mişcarea liniară.

În acest scop, să revenim la mişcarea liniară analizată în subparagraful 13.4.1din [1] şi să ne oprim la relaţia (13.31), care exprimă energia de mişcare gravitaţională a masei m prin produsul mar_m, în care a este acceleraţia, iar r_m este distanţa parcursă în mişcare.(A se vedea şi postarea „Legea fundamentală amişcării” tot pe acest blog).

În continuare, înscriind mişcarea într-un sistem de coordonate carteziene cu originea în punctul de pornire în mişcare a masei m şi renunţând la indicele m, pentru simplificare, distanţa parcursă r are coordonatele x, y, z, iar relaţia (13.31) se transcrie astfel:

        (12)

Conform [2], din tabelul derivatelor principalelor funcţii de la pag. 307, scoatem formula de derivare a funcţiei radical din x,

       (13)

Pe baza relaţiilor (13) şi (7), derivatele parţiale ale energiei cinetice E_c din relaţia (12) sânt date de expresiile:

       (14)

   

        (15)

  

         (16)

  

Conform expresiilor (14), (15) şi (16), gradientul energiei cinetice de mişcare a masei m în câmp gravitaţional este dat de relaţia

 (17)

   

Cum numărătorul relaţiei (17) reprezintă energia cinetică E_c, conform relaţiei (12), iar numitorul reprezintă distanţa r parcursă în mişcare de masa m, fracţia din membrul drept reprezintă chiar forţa care mişcă masa m, adică

        (18)

   

Prin urmare, atât în mişcarea de rotaţie cât şi în mişcarea liniară, forţa de mişcare este gradientul energiei pe care o mişcă şi generalizăm această definiţie în concluzia:

b)      Forţa care produce mişcarea, indiferent dacă forma de mişcare este liniară sau de rotaţie şi indiferent dacă se mişcă masă sau energie sau o combinaţie a lor, reprezintă gradientul energiei mişcate. 

În fine, pentru ca vectorul gradient al energiei mişcării liniare să aibă un potenţial vectorial, trebuie ca divergenţa acestuia să fie nulă, conform [3]paragraful 3.2.18.

Conform [3], paragraful 3.2.11, divergenţa vectorului grad f se obţine ca sumă a derivatelor parţiale ale componentelor vectoriale.

Conform [2],pag. 309 pct. 4), derivata unei fracţii se calculează cu formula:

      (19)

Calculul derivatelor parţiale din expresia (12), conform relaţiei (19),cu luarea în considerare şi a relaţiilor (14), (15) şi (16), conduce la suma diferită de zero

  

     (20)

care arată căgradientul energiei cinetice, în mişcarea liniară a energiei, nu are potenţial vectorial deoarece divergenţa gradientului este diferită de zero.

Prin urmare, să reţinem încă o concluzie de importanţă deosebită:

c)      Mişcarea liniară a energiei se produce ca o simplă curgere liniară, fără perturbaţii turbionare în planul perpendicular pe direcţia mişcării, divergenţa vectorului gradient al energiei mişcării liniare fiind diferită de zero.

Dacă, aşa cum s-a demonstrat, mişcarea liniară a energiei se produce fără perturbaţii turbionare în planul perpendicular pe direcţia mişcării, cu totul altfel stau lucrurile în mişcarea de rotaţie a energiei.

Conform celor demonstrate în paragraful 5.3 din [1], în mişcarea de rotaţie a energiei, gradientul energiei giroscopice are şi divergenţa şi rotorul nule, relaţiile (5.33) şi (5.34). (A se vedea şi postarea „Mișcarea derotație” tot pe acest blog).
Având divergenţa nulă, gradientul energiei giroscopice are potenţial vectorial, iar în paragraful 5.5 din [1] a fost determinat acest potenţial vectorial, prin relaţia (5.57).

Existenţa potenţialului vectorial în mişcarea de rotaţie a energiei dovedeşte că aceasta este însoţită şi de o mişcare turbionară în planul perpendicular pe direcţia de mişcare de rotaţie, fapt demonstrat în paragrafele următoare ale capitolului 5 din [1], fiind factorul care determină formarea şi existenţa găurii centrale lipsită de energie, în lungul axei de rotaţie a structurii de energie cu mişcare de rotaţie, cu forma de clepsidră. Conform celor arătate în subparagraful 6.1.4.3, mişcarea turbionară ce însoţeşte mişcarea de rotaţie produce o configurare diferită a aştrilor în zona centrală a unei galaxii şi în vecinătatea găurii lipsite de energie. (A se vedea şi postarea „Mișcarea de rotație” tot pe acest blog).     

În încheiere, să mai reţinem încă o concluzie deosebit de importantă:

d)      Mişcarea de rotaţie a energiei este însoţită şi de o mişcare turbionară ce se se produce în planul perpendicular pe direcţia mişcării de rotaţie. Această mişcare turbionară este cauza formării şi existenţei găurii centrale lipsite de energie dispusă în lungul axei de rotaţie şi în formă de clepsidră.  

Concluziilec)şi d) au implicaţii în înţelegerea naturii undelor electromagnetice. Conform concluziei c), dacă unda electromagnetică se propagă ca o curgere liniară de energie, pe durata propagării, unda nu este însoţită de perturbaţii turbionare în planul perpendicular pe direcţia de propagare, deci este o undă doar electrică şi nu electromagnetică, ceea ce nu corespunde realităţii.

Rezultă, conform concluziei d), că unda electromagnetică nu este o curgere liniară de energie, ci o emisie dirijată de structuri de energie care-şi menţin forma şi caracteristicile şi în drumul de propagare. Asemenea structură de energie a fost analizată în paragraful 5.10 „Fotonul – structura elementară (fundamentală) de energie”. (A se vedea şi postarea „Fotonul” tot pe acest blog).

Prin urmare, unda electromagnetică este o emisie dirijată de fotoni, iar caracterul oscilant îi este dat de numărul variabil (oscilant) de fotoni emişi simultan. 

Aşadar, reţinem şi concluzia:

e)      Unda electromagnetică este o emisie dirijată de fotoni, structuri care îşi menţin caracteristicile pe durata şi pe drumul de propagare. Caracterul oscilant al undei electromagnetice este dat de cantitatea oscilantă de fotoni emisă simultan. 

În fine, concluzia c) permite o remarcă şi asupra undelor scalare.Cum undele scalare produc doar mişcări liniare de energie, conform concluziei c), ele nu sânt însoţite de perturbaţii turbionare în planul perpendicular pe direcţia mişcării energiei, ceea ce le deosebeşte de undele electromagnetice. (A se vedea şi postarea „Undelescalare” tot pe acest blog).

2  Forţe naturale şi forţe create

În finalul paragrafului 13.4 din [1], s-a vorbit de forţe naturale şi de forţe create şi considerăm necesare cîteva explicaţii suplimentare.

Prin forţe naturale înţelegem toate forţele care se manifestă în natură, pe planeta nostră sau în cosmos, în mod necesar şi obiectiv, drept consecinţe ale manifestărilor legilor fundamentale în interacţiunile dintre diferitele corpuri sau structuri materiale sau de energie existente în mod obiectiv în Univers şi în spaţiul înconjurător. Asemenea forţe se manifestă la nivel microcosmic, în toate structurile atomice şi moleculare, la nivel planetar, în scoarţa terestră, în apa râurilor, mărilor şi oceanelor şi în atmosfera înconjurătoare, la nivelul sistemului planetar, pe fiecare planetă şi în interacţiunile dintre ele şi dintre ele şi aştrii centrali, la nivel galactic, atât în interiorul galaxiilor cât şi în interacţiunile dintre galaxii.

Iar prin forţe create înţelegem forţele care apar tot datorită legilor fundamentale, dar în interacţiunile fie din interiorul lumii vii, fie dintre lumea vie şi natura înconjurătoare. Fiind provocate de elemente ale lumii vii, aceste forţe au mai fost numite şi forţe provocate, dar pot fi numite şi forţe vii, pentru că se manifestă în interiorul organismelor vii, în interacţiunile dintre organismele vii şi în interacţiunile acestora cu mediul înconjurător, asigurându-le existenţa sau periclitându-le existenţa.

Forţele vii au evoluat concomitent cu evoluţia lumii vii, atât ca formă şi intensitate cât şi ca mod de aplicare. Izvorul evoluţiei forţelor vii este învăţarea, cunoaşterea. Pe măsura învăţării şi cunoaşterii lumii înconjurătoare se perfecţionează formele, intensitatea şi metodele de aplicare a forţelor vii şi se îmbunătăţesc rezultatele obţinute. Exemplele sânt pretutindeni în jurul nostru şi uşor de perceput de către oricine, indiferent de vârstă sau de pregătire. Tocmai această prezenţă masivă şi cotidiană ne împiedică uneori să înţelegem importanţa învăţării şi cunoaşterii pentru îmbunătăţirea propriei vieţi.

Aşa cum izvorul evoluţiei forţelor vii este învăţarea şi cunoaşterea, la rândul lor, forţele vii sânt izvorul evoluţiei economico-sociale a societăţii. De aceea, învăţarea şi cunoaşterea, prin perfecţionarea continuă a forţelor vii, sânt şi factorul fundamental al evoluţiei societăţii.

Atât în epoca numită a sălbăticiei cât şi în epoca organizării gentilice, învăţarea şi cunoaşterea au fost bunuri ale întregii comunităţii, fiind însuşite de fiecare individ. Explicaţia este simplă: productivitatea fiind mică, la producerea celor necesare vieţii, trebuiau să participe toţi membrii colectivităţii, ceea ce presupunea ca toţi să aibă cunoştinţele necesare desfăşurării diverselor activităţi. Orice nouă cunoştinţă, deprindere sau procedeu găsite de un membru al colectivităţii erau împărtăşite tuturor membrilor şi în scurtă vreme deveneau bunuri câştigate de întreaga comunitate.

Cu totul altfel stau lucrurile în epoca civilizaţiei, care a urmat organizării gentilice. Omul putând produce mai mult decât consuma, a devenit el însuşi o marfă şi a apărut sclavia. Ulterior sclavia a fost înlocuită cu iobăgia, aceasta înlocuită şi ea cu munca salarială, dar majoritatea populaţiei a rămas tot o marfă căreia i s-a permis atâta învăţare şi cunoaştere cât să îndeplinească însărcinările stăpânirii.

De-a lungul întregii epoci a aşa-zisei civilizaţii, învăţarea şi cunoaşterea au fost apanajul unor cercuri elitistegrupate în jurul puterii. Ba chiar mai mult, de câteva sute de ani, descoperirile sânt brevetate, fapt ce restrânge şi mai mult aplicabilitatea lor şi constituie o contradicţie între dezvoltarea forţelor vii şi utilitatea lor socială.

După rezultatul lor, forţele vii pot fi clasificate ca folositoare, dăunătoare şi periculoase, fără a putea demarca graniţe precise între ele, pentru că rezultatul unei interacţiuni poate fi benefic unei părţi, dar dăunător sau periculos pentru cealaltă parte. Printre forţele vii periculoase pot fi enumerate războaiele şi poluarea. Dacă multe secole şi milenii poluarea n-a avut un impact semnificativ nici asupra mediului înconjurător şi nici asupra societăţii, în prezent, prin creşterea vertiginoasă a forţelor vii, poluarea a devenit principalul factor nociv pentru om şi pentru societate, manifestându-se atât asupra mediului înconjurător cât şi asupra sănătăţii şi dezvoltării omului prin aerul inspirat, prin apa băută, prin alimentele mâncate, prin medicamentele consumate şi prin câmpurile de energie cu care este continuu bombardat.

Dar despre toate acestea, mai pe larg, în capitolele următoare.În încheiere, o concluzie asupra condiţiilor optime de dezvoltare atât a forţelor vii cât şi a societăţii:

f)       Condiţiile optime de dezvoltare atât a forţelor vii cât şi a omului şi a societăţii sânt:

-        cuprinderea întregii populaţii în procesul de învăţare şi de cunoaştere şi

-        dezvoltarea şi aplicarea forţelor vii în deplină armonie cu forţele obiective ce acţionează în natură şi în mediul înconjurător. 

Bibliografia

1 CONSTANTIN TEODORESCU:     Structură şi evoluţie. Editura MATRIX ROM.

   Bucureşti 2015.Ediţia a 4 – a revizuită şi adăugită. Se află la Biblioteca Naţională, la Biblioteca     
   Centrală Universitară Carol I şi la Biblioteca Centrală a Zniversităţii Politehnica Bucureşti.

2 BRONŞTEIN I.N. şiSEMENDIAEV K. A.:Spravocinik po matematike dlia injenerov i

    uciaşcihsiavtuzov. Izdatelstvo “Nauka”. Moskva 1964.

3 ANDRE ANGO:Matematika dlia electro - i radioinjenerov.Perevod s franţuscovo (André

   ANGOT). Izdatelstvo “Nauka”. Glavnaia redakţia fizico – matematiceskoi literaturî.

   Moscva, 1967.