Mişcarea giroscopică cu precesie

Autor: ing. Constantin Teodorescu

Articolul "Mişcarea giroscopică cu precesie" prezintă principalele aspecte şi caracteristici ale mişcării giroscopice cu precesie, forma fundamentală a mişcării corpurilor materiale în Univers, demonstrate cu prioritate de autor, în studiul "Structură şi evoluţie".

Cuprins:

1  Sistemele de coordonate şi unghiurile lui Euler

2  Energia giroscopică a corpului material giroscopic cu precesie

3  Câmpul vectorial al energiei giroscopice a corpului material giroscopic cu precesie

4  Dependenţa energiei giroscopice de unghiul de nutaţie J

5  Mişcarea giroscopică cu precesie însoţită de o mişcare liniară

1  Sistemele de coordonate şi unghiurile lui Euler

Corpul material giroscopic analizat în capitolul 2.2 din [1] a fost considerat un corp material giroscopic cu precesie nulă, adică axa de simetrie 0z, în jurul căreia corpul se roteşte, îşi păstrează neschimbată direcţia, rămânând stabilă.

În [2], capitolul VI, este prezentată condiţia stabilităţii axei de rotaţie astfel:

“Un giroscop căruia i s-a dat o mişcare de rotaţie în jurul axei sale de simetrie, îşi păstrează neschimbată direcţia acestei axe, în cazul când momentul tuturor forţelor exterioare în raport cu punctul fix 0 este nul”, adică M₀ = 0.

În univers nu există corpuri materiale izolate, corpuri materiale care să nu fie supuse unor influenţe externe. De aceea, analiza din capitolul 2.2 trebuie privită ca un caz particular, dar pe deplin posibil în cazul în care forţele externe se anihilează reciproc.

În realitate, fie sub influenţe externe, fie ca urmare a propriei rotaţii în jurul unui corp central, aşa cum s-a arătat în ultimul subparagraf al subcapitolului 2.2, corpul material giroscopic este supus la o mişcare nouă, suplimentară, care constă în rotirea axei 0z a giroscopului în jurul unei alte axe 0z₁ fixă, numită mişcare de precesie, cu o altă viteză de rotaţie w₁ diferită de w. Această mişcare giroscopică cu precesie este analizată în subcapitolul 2.3 din [1].

La începutul acestei analize, vom urma analiza din [3], paragraful 36.

Fiind vorba de două mişcări de rotaţie diferite, se folosesc două sisteme de coordonate cu aceeaşi origine: unul fix, iar altul mobil şi legat invariabil de corpul material giroscopic.

Sistemul fix, notat cu 0xyz, are versorii i, j, k. Corpul material giroscopic, cu centrul în 0, se roteşte cu viteza unghiulară , în jurul axei 0z.

Sistemul mobil, notat cu 0x₁y₁z₁, are versorii i₁, j₁, k₁ şi originea tot în 0. Fiind invariabil legat de corpul material giroscopic, sistemul mobil se roteşte, împreună cu acesta, în jurul punctului 0, astfel încât axa de simetrie 0z a corpului material giroscopic execută o mişcare de rotaţie în jurul axei fixe 0z₁, cu viteza unghiulară w₁, diferită de viteza unghiulară w a giroscopului, ca în fig. 1. 

Fig. 1.  Sistemele de coordonate ale corpului material giroscopic. Unghiurile lui Euler.

În [3], paragraful 36, se demonstrează relaţiile dintre coordonatele x₁, y₁, z₁ din sistemul de coordonate mobil şi coordonatele x, y, z din sistemul de coordonate fix, pentru acelaşi punct din spaţiu. Aceste relaţii sânt de forma:

(1)

Coeficienţii din partea dreaptă a ecuaţiilor (1) sânt exprimaţi, în funcţie de “unghiurile lui Euler” j, y şi J, prin expresiile:

(2)

Unghiurile lui Euler, aşa cum se poate observa şi pe fig. 1, au următoarea reprezentare:

-        reprezintă rotaţia în planul x0y în jurul axei 0z;

-        reprezintă rotaţia în planul x₁0y₁ în jurul axei 0z₁, numit şi unghiul de precesie;

-        reprezintă unghiul dintre axele 0z şi 0z₁, numit şi unghiul de nutaţie.

În funcţie de timp, unghiurile lui Euler se exprimă prin relaţiile:

(3)

(4)

Unghiul de nutaţie variază în timp numai în funcţie de variaţia în timp a influenţelor externe. Atâta timp cât rezultanta influenţelor externe este constantă şi unghiul de nutaţie este constant.

2  Energia giroscopică a corpului material giroscopic cu precesie

2.1  Componentele mişcării giroscopice cu precesie

Elementul de masă al corpului material giroscopic cu precesia diferită de zero execută, simultan, două mişcări de rotaţie: una în jurul axei 0z cu viteza de rotaţie w şi una în jurul axei 0z₁ cu viteza de rotaţie w₁.

Energia giroscopică a elementului de masă m, în mişcarea de rotaţie în jurul axei 0z, notată cu e_gz, este exprimată prin relaţia (2.2.3) din [1], faţă de axa 0z:

(5)

Energia giroscopică a aceluiaşi element de masă m, în mişcarea de rotaţie în jurul axei 0z₁, notată cu e_gz1, este exprimată tot prin relaţia (2.2.3) din [1], dar faţă de axa 0z₁, şi are forma:

(6)

Energia giroscopică totală a elementului de masă m însumează energiile giroscopice proprii celor două mişcări de rotaţie simultane, adică

(7)

Conform relaţiilor (5) şi (6), ambele energii e_gz şi e_gz1 au suprafeţe de nivel energetic constant de formă cilindrică, de raze r_z şi r_z1, în jurul axelor 0z şi 0z₁. Cum axele lor formează unghiul J, intersecţiile suprafeţelor cilindrice de nivel energetic constant sânt linii curbe cu forme care depind de razele r_z şi r_z1 şi de unghiul J.

Prin urmare, corpul material giroscopic cu precesie nu are suprafeţe de nivel energetic constant, ci doar linii de forme determinate de razele r_z şi r_z1 şi de unghiul J.   

2.2  Expresia generală a distanţei elementului de masă m(x, y, z) faţă de axa 0z₁

Distanţa elementului de masă m la axa 0z₁, r_z1, în funcţie de coordonatele elementului de masă m şi de unghiurile lui Euler, poate fi exprimată algebric sau geometric.

Prima cale necesită calcule pe baza relaţiilor (1) şi (2). Aceste calcule sânt mai complicate, ca scriere, şi, din această cauză, sânt prezentate în Anexa 2.3.1: “Calculul algebric al energiei giroscopice totale a elementului de masă” din [1]. 

Cea de a doua cale este mai puţin laborioasă şi este prezentată în continuare.

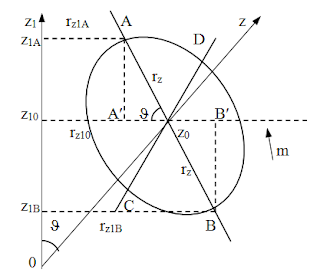
Se consideră planul z₁0z, format de axele z₁ şi z, care subîntind unghiul J, ca în figura 2.

Fig. 2.  Exprimarea r_z1minim şi r_z1maxim, prin raţionamente geometrice.

Elementul de masă m, în mişcarea sa giroscopică în jurul axei z, parcurge cercul m, de rază r_z şi cu centrul în z₀, situat într-un plan perpendicular pe axa z. În cercul m, se consideră diametrul AB, care este paralel cu axa 0x şi este conţinut în planul z₁0z, şi diametrul CD, care este perpendicular pe diametrul AB şi paralel cu axa 0y. Din punctul A se coboară perpendiculara AA¢ pe z₁₀z₀ şi se formează dreptunghiul z_1AAA¢z₁₀ şi triunghiul dreptunghic AA¢z₀. Triunghiul dreptunghic AA¢z₀ este asemenea cu triunghiul dreptunghic 0z₁₀z₀, unghiurile z₀0z₁₀ şi A¢z₀A fiind egale cu J, ca unghiuri cu laturile perpendiculare.

Din triunghiul dreptunghic 0z₁₀z₀, se exprimă cateta z₀z₁₀, r_z10, prin relaţia

 (8)

Din triunghiul dreptunghic AA¢z₀, se exprimă cateta A¢z₀, prin relaţia

(9)

Evident, distanţa punctului A la axa 0z₁ este dată de diferenţa:

(10)

În mod similar se exprimă şi distanţa punctului B la axa 0z₁, prin suma:

(11)

În continuare, pentru a nu îngrămădi figura 2, dezvoltăm raţionamentul geometric pe figura 3.

Fig. 3.  Exprimarea r_z1P, prin raţionamente geometrice.

În figura 3, prin punctul curent P, în care se află elementul de masă m la un moment dat, se duce coarda PP¢, paralelă cu diametrul CD. Mijlocul coardei PP¢, intersecţia cu diametrul AB, se noteză cu R. Prin R se duce perpendiculara pe axa 0z₁, care cade în punctul z_1P. Se uneşte punctul z_1P cu punctul P şi se obţine distanţa r_z1P a punctului P la axa 0z₁ (Pz_1P este perpendicular pe 0z₁, conform teoremei celor trei perpendiculare). Din punctul R se coboară perpendiculara, în planul z0z₁, care intersecteză pe z₀z₁₀ în punctul S. S-a obţinut triunghiul dreptunghic RSz₀, cu ipotenuza Rz₀ = x_P, din care rezultă:

(12)

Din dreptunghiul RSz₁₀z_1P, rezultă

 (13)

şi, conform relaţiilor (8) şi (12) 

(14)

unde j este unghiul dintre direcţiile z₀A şi z₀P.

Din triunghiul dreptunghic PRz₀, se deduce

(15)

În fine, din triunghiul dreptunghic PRz_1P, în care se cunosc catetele Rz_1P, relaţia (14), şi PR, relaţia (15), se exprimă ipotenuza Pz_1P = r_z1P, care este distanţa punctului P la axa 0z₁:

(16)

Pentru j egal cu 0 sau cu p, evident, relaţia (16) se transformă în relaţia (10) sau în relaţia (11).

Pe baza relaţiilor 

(17)

relaţia (16) se transcrie în coordonate carteziene astfel:

(18)

Prin urmare, relaţiile (16) şi (18) reprezintă expresia generală a pătratului distanţei punctului curent P al cercului m, la axa 0z₁, în coordonate polare, respectiv, în coordonate carteziene.

Înainte de a merge mai departe cu analiza, să observăm că punctul P¢, simetricul punctului P faţă de diametrul AB, are aceeaşi distanţă faţă de axa 0z₁ ca şi punctul P.

În fine, o ultimă observaţie: faptul că distanţa punctului curent P al cercului m, la axa 0z₁, nu depinde de unghiul de precesie y nu trebuie să surprindă, deoarece mişcarea punctului P pe cercul m depinde doar de unghiul de nutaţie J, indiferent de poziţia cercului m în jurul axei 0z₁.

2.3 Expresia energiei giroscopice totale a elementului de masă

Prin introducerea relaţiei (16) în relaţia (7) se obţine expresia energiei giroscopice totale a elementului de masă în mişcarea giroscopică cu precesie, exprimată în coordonate polare, sub forma

(19)

iar prin introducerea relaţiei (18) în relaţia (7), se obţine şi exprimarea în coordonate carteziene, sub forma

(20)

Expresia energiei giroscopice totale a elementului de masă în mişcarea giroscopică cu precesie, exprimată fie în coordonate polare, relaţia (19), fie în coordonate carteziene, relaţia (20), are caracter universal deoarece:

-        reprezintă relaţia de bază şi primordială dintre masa şi energia internă a elementului de masă, sub influenţă externă, pe de o parte, şi

-        este prezentă totdeauna şi pretutindeni în univers, pe de altă parte.

 Energia giroscopică totală a elementului de masă al corpului material cu mişcare giroscopică cu precesie, aşa cum se poate observa cu uşurinţă din relaţia (19), are trei componente:

a)      O componentă continuă, notată cu e_gc, care conţine doar termenii ce nu depind de j, adică

          (21)

exprimată în unităţi de energie şi determinată de vitezele de rotaţie şi , de coordonatele x, y, z ale elementului de masă şi de unghiul de nutaţie J.

b  Două componente ondulatorii sinusoidale: 

-        una în planul xy, determinată de viteza de rotaţie a mişcării de precesie, de unghiul de nutaţie şi de mişcarea elementului de masă în planul x0y, exprimată prin relaţia

(22)

           

            în care fracţia reprezintă amplitudinea oscilaţiilor date de factorul cosj;

-    a doua, determinată tot de viteza de rotaţie a mişcării de precesie, de unghiul de nutaţie şi de mişcarea elementului de masă în planul x0y, dar care depinde şi de coordonata z şi se produce ortogonal pe planul x0y şi paralel cu axa 0z, exprimată prin relaţia

    (23)

în care fracţia reprezintă, de asemenea, amplitudinea oscilaţiei dată de factorul cosj.

Nota 1:     Se cuvine menţionat faptul că în [2], capitolul VI, este demonstrată mişcarea ondulatorie a componentelor w_x şi w_y, într-o demonstraţie mai amplă, prin care se determină condiţiile ca axa de simetrie în jurul căreia se roteşte giroscopul să fie fixă.

Cu ajutorul relaţiei (3) şi al relaţiilor

(24)

din [4], mişcare mecanică, componentele ondulatorii ale energiei totale a elementului de masă al corpului material cu mişcare giroscopică cu precesie pot fi exprimate în funcţie de timpul t, de frecvenţa n, de perioada T sau de viteza v.

Componenta ondulatorie din planul x0y este pulsatorie, de semn pozitiv, asemenea unei oscilaţii electrice la ieşirea dintr-un redresor cu diode şi fără condensator, datorită pătratului funcţiei cosinusoidale.

Cele două componente ondulatorii, una în planul x0y şi alta ortogonală pe ea, în planul x0z, ale energiei totale a elementului de masă al corpului material cu mişcare giroscopică cu precesie sânt determinate strict de mişcarea de precesie a corpului material giroscopic.

Elementul de masă al corpului material giroscopic, care execută o mişcare giroscopică cu precesie, câştigă energie în mişcarea de îndepărtare de axa de precesie 0z₁ şi pierde energie în mişcarea de apropiere de axa de precesie. Energia câştigată este luată din energia externă care îi provoacă mişcarea de precesie, iar energia pierdută este cedată tot acestei energii externe. Câştigarea şi pierderea de energie sânt fenomene succesive în timp pentru elementul de masă P, dar simultane pentru elementele de masă P şi P’ simetrice faţă de diametrul AB, fapt ce face ca în energia externă să se manifeste şi să se propage, îndepărtându-se de corpul material giroscopic, o undă complexă în planurile x0y şi x0z.

Într-adevăr, dacă urmărim mişcarea elementului de masă m pe semicercul ACB (a se vedea fig. 3), se observă, cu uşurinţă, că energia totală giroscopică a acestuia se măreşte continuu, de la minimă, în punctul A, la maximă, în punctul B. În continuare, pe semicercul BDA, energia totală giroscopică a elementului de masă scade continuu, de la maximă, în punctul B, la minimă, în punctul A. 

Dacă se anulează mişcarea de precesie, adică J = 0 şi, implicit, w₁ = 0, expresia energiei giroscopice totale a elementului de masă al corpului material cu mişcare giroscopică devine

(25)

expresie identică cu (2.2.3) din [1]. În acest caz, componentele ondulatorii dispar şi rămâne doar componenta continuă care reprezintă energia elementului de masă al corpului material cu mişcare giroscopică fără precesie.

Din relaţiile (19) – (23) mai rezultă şi aspectul: orice modificare a mişcării de precesie (a unghiului de nutaţie J) conduce la modificarea simultană a componentelor ondulatorii ortogonale pe coordonatele x (în planul x0y) şi z (în planul xoz) ale energiei giroscopice totale a elementului de masă al corpului material giroscopic cu mişcare de precesie, indiferent de modul în care s-a făcut modificarea.

Ba mai mult, modificarea uneia dintre componentele ondulatorii ortogonale atrage după sine şi modificarea celeilalte componente ondulatorii.

Nota 2:  Asemenea fenomene se petrec în electromagnetism, prin legăturile şi condiţionarea reciprocă dintre câmpurile electric şi magnetic.

               

Prin urmare, cu toată certitudinea, putem formula următoarele concluzii fundamentale:

1)      Mişcarea giroscopică cu precesie este forma fundamentală de mişcare în univers, deoarece permite:

-    conservarea în timp a energiei giroscopice;

-    evoluţia în cadrul interacţiunii cu corpuri externe;

-    reacţii adecvate la orice modificare a influenţelor externe, adică la orice modificare a mediului extern.

2)      Reacţiile sânt de aşa natură şi de o astfel de intensitate încât să menţină stabilitatea şi să permită evoluţia sistemului.

3)      Legăturile între diferitele corpuri materiale giroscopice se realizează prin câmpuri de energie care conţin şi ansambluri de unde spaţiale compuse din unde plane ortogonale.

În [1], la finalul paragrafului, au fost determinate şi maximele şi minimele energiei giroscopice cu precesie.

Conform [5], paragraful 162, o funcţie de mai mute variabile poate atinge un maxim sau un minim numai la acele valori ale variabilelor pentru care derivatele parţiale de ordinul întâi sânt nule sau nu există. Funcţia are maxim dacă derivatele parţiale de ordinul doi sânt negative sau nule şi are minim dacă derivatele parţiale de ordinul doi sânt pozitive sau nule.

După efectuarea calculelor, s-au obţinut rezultatele prezentate în concluziile:

1)      Singurul punct cu energia giroscopică nulă este centrul corpului material giroscopic, care are coordonatele x = y = z = 0.

2)      În planul x0z, pentru care y = 0, energia giroscopică are valori minime de-a lungul dreptelor x₁ = k₁z şi x₂ = k₂z, cu   

        (26)

Dreptele x₁ şi x₂ depind de parametrii w, w₁ şi de unghiul de nutaţie J. Aceşti parametri, în analiza valorilor de maxim şi de minim ale energiei giroscopice a corpului material giroscopic executată mai sus, au fost consideraţi că rămân nemodificaţi. În realitate, evoluţia în cadrul mişcării giroscopice cu precesie are loc tocmai prin modificarea acestor parametri.

2.4  Analiza expresiilor energiei giroscopice obţinute prin metoda geometrică şi prin metoda unghiurilor lui Euler

În Anexa 2.3.1 din [1], s-a obţinut expresia energiei giroscopice totale în funcţie de coordonatele elementului de masă şi de unghiurile lui Euler, plecându-se de la relaţiile (1) şi (2), sub forma:

(27)

Prin urmare, relaţiile (19) şi (27) sânt compatibile doar referitor la componenta continuă a energiei giroscopice totale şi sânt incompatibile referitor la componentele ondulatorii, pe care relaţia (27) le neglijează, nu le evidenţiază.

3  Câmpul vectorial al energiei giroscopice a corpului material giroscopic cu precesie

3.1  Gradientul energiei giroscopice a corpului material giroscopic cu precesie

Vom analiza gradientul energiei giroscopice totale a elementului de masă al corpului material giroscopic cu precesie, exprimată prin relaţia (20), dar pe care o transformăm prin separarea pe coordonatele x, y şi z, astfel:

  (28)

Componentele gradientului de-a lungul axelor de coordonate sânt:

(29)

(30)

(31)

Iar gradientul energiei giroscopice totale a elementului de masă al corpului material giroscopic cu precesie, în coordonate carteziene, este exprimat prin relaţia

 (32)

sau, în coordonate polare pe cercul m, prin relaţia

 (33)

Gradientul reprezintă forţa centrifugă şi din relaţiile (32) şi (33), rezultă concluziile:

6)      Pe parcursul mişcării de rotaţie în jurul axei 0z, componentele gradientului energiei giroscopice totale a elementului de masă al corpului material giroscopic cu precesie au o evoluţie oscilatorie, astfel:

-       cosinusoidal pe axa 0x,

-       sinusoidal pe axa 0y şi

-       cosinusoidal pe axa 0z.

Pe axele 0x şi 0z, componentele sânt modulate oscilatoriu.

7)      Oscilaţiile componentelor gradientului energiei giroscopice sânt sincrone cu oscilaţiile energiei giroscopice totale a elementului de masă.

8)      Ca urmare a evoluţiei oscilatorii sincrone cu energia giroscopică totală, gradientul energiei giroscopice totale a elementului de masă al corpului material giroscopic cu precesie execută o rotaţie sincronă cu elementul de masă în jurul axei 0z, dar complexă: o rotaţie completă paralelă cu planul ecuatorial (xy), de forma unui oval închis, concomitentă cu o rotaţie completă în planul meridian (xz), însoţită de o alunecare în lungul axei z.

9)      Dependenţa gradientului energiei giroscopice de mărimile vectoriale şi şi de unghiul de nutaţie J, pe lângă parametrii de poziţie x, y, z sau r, j, q, asigură mişcării giroscopice cu precesie o largă varietate de forme de manifestare, atât la scară cosmică cât şi la scară atomică, varietate manifestată şi prin complexitatea lumii în care trăim.  

Din aceste concluzii rezultă că mişcarea giroscopică cu precesie generează, în spaţiul ocupat de corpul material, două câmpuri sincrone:

-        un câmp scalar al energiei giroscopice a elementului de masă şi

-        un câmp vectorial al gradientului energiei giroscopice.

Fiecărui punct din spaţiul corpului material îi corespund caracteristicile:

-        o energie giroscopică de mărime determinată de poziţia sa, şi

-        un gradient al energiei giroscopice cu mărimea şi direcţia determinate, de asemenea, de poziţia sa.

În mişcarea de rotaţie în jurul axei 0z, elementul de masă al corpului material giroscopic ia, pe rând, caracteristicile punctelor din spaţiu pe care le parcurge.

Prin urmare, desprindem şi concluzia:

10)  Sincronizarea gradientului cu energia giroscopică arată  că, de fapt, energia giroscopică totală a elementului de masă  şi gradientul său devin (se transformă în) proprietăţi ale spaţiului ocupat de corpul material giroscopic cu precesie, proprii fiecărui punct al acestuia, iar elementul de masă, în mişcarea sa giroscopică, ia, pe rând, energia şi gradientul punctelor pe care le parcurge.

În [1], subcapitolul 2.3, s-a mai demonstrat că:

11)  Singurul punct cu gradientul energiei giroscopice nul este centrul corpului material giroscopic, care are coordonatele x = y = z = 0.

12)  În planul x0z, pentru care y = 0, gradientul energiei giroscopice are valori minime de-a lungul dreptelor x₃ = k₃ z şi x₄ = k₄ z, cu 

(34)

Dreptele x₃ şi x₄ depind de parametrii w, w₁ şi de unghiul de nutaţie J într-o formă mai complexă ca dreptele x₁ şi x₂ definite prin coeficienţii daţi de relaţiile (26). 

Compararea coeficienţilor k₃ şi k₄ cu coeficienţii k₁ şi k₂ arată că dreptele de-a lungul cărora gradientul energiei giroscopice are valori minime sânt diferite de dreptele de-a lungul cărora energia giroscopică are valori minime.

3.2  Planul în care se află vectorul gradient

Pentru a determina planul în care se află vectorul gradient, revenim la relaţia (33), pe care o punem sub forma

(35)

care, pe baza relaţiilor (17), (18) şi figurii 3, devine

(36)

Conform relaţiei (36), vectorul grad e_g este suma a doi vectori gradient corespunzători energiilor giroscopice ale elementului de masă faţă de axa giroscopică z şi faţă de axa de precesie z₁. Vom nota aceşti vectori cu g_z şi, respectiv, g_z1, adică

(37)

Ambii vectori g_z şi g_z1 au punctul de aplicaţie în elementul de masă m, adică în punctul P, şi au direcţiile în prelungirea razelor giroscopice r_z şi r_z1, aşa cum se arată în figura 4.

Fig. 4.  Vectorii gradient g_z şi g_z1 şi grad e_g.

În [1], subcapitolul 2.3, s-a mai demonstrat că:

13)  Rotirea giroscopică a elementului de masă în jurul axei z, pe cercul m, este însoţită de rotirea sincronă a gradientului energiei giroscopice a elementului de masă.

14)  Rotaţia giroscopică a elementului de masă se produce într-unul şi acelaşi plan, planul xy perpendicular pe axa z.

15)  Rotaţia gradientului energiei giroscopice a elementului de masă este o rotaţie complexă care se produce simultan atât în plan orizontal cât şi în plan vertical, în ambele planuri rotaţia fiind de 360⁰. Rotaţia gradientului este o răsucire continuă în plan orizontal şi în plan vertical. Ba chiar mai mult, rotaţia în plan vertical se produce simultan cu o glisare pe axa z₁, între limitele z₁₀ ± r_z sinJ, într-o rotaţie parcurgându-se acest interval în ambele sensuri (dus pe arcul ACB – întors pe arcul BDA).

16)  Rotaţia gradientului energiei giroscopice a elementului de masă m se produce, pe circumferinţa m, simultan cu variaţia mărimii sale de la valoarea minimă la valoarea maximă, pe semicircumferinţa ACB, şi de la valoarea maximă la valoarea minimă, pe semicircumferinţa BDA.

17)  Rotaţia complexă a gradientului energiei giroscopice a elementului de masă, care se produce simultan atât în plan orizontal cât şi în plan vertical, în ambele planuri rotaţia fiind de 360⁰, privită pe ansamblul paraleleor şi meridianelor corpului material giroscopic cu precesie, conduce la prezenţa vectorului gradientului energiei giroscopice în toate punctele spaţiului corpului material, pe toate direcţiile şi de mărime determinată de poziţia punctului considerat, de mărimile vitezelor giroscopice şi de precesie  w şi w₁ şi de unghiul de nutaţie J.

S-ar părea că avem o imagine completă asupra gradientului energiei giroscopice a corpului material giroscopic cu precesie, dar mai trebuie cercetat un aspect: trebuie cercetat gradientul şi pe paralelele de latitudine J, figura 5. 

Fig. 5.  Paralela J parcursă de punctul P.

Pentru toate punctele cercului m(J), raza vectoare 0P formează un unghi J cu axa z şi din triunghiul dreptunghic 0z_qP rezultă

(38)

Prin introducerea relaţiei (38), coroborată cu relaţiile (17), în relaţia (19) a energiei giroscopice, aceasta ia forma

(39)

Particularitatea relaţiei (39) constă în existenţa de oscilaţii în cuadratură în planul yz, conţinute în paranteza rotundă. Oscilaţiile în cuadratură, fiind proporţionale cu suma pătratelor sinusului şi cosinusului unghiului j, cu diferenţa de fază de p/2, constituie o premisă pentru producerea de mişcări turbionare în zona paralelelor de latitudine ± J.

Nota 3:  Oscilaţiile în cuadratură ale energiei giroscopice a Pământului, în zona paralelor de 23⁰ latitudine nordică şi sudică, reprezintă principala premisă pentru fenomene ca cele manifestate în Triunghiul Bermudelor şi în Marea Diavolului, prin producerea cicloanelor devastatoare, şi chiar pentru aspecte caracteristice Saharei şi altor zone de la tropice. Pentru producerea fenomenelor caracteristice acestor zone, pe lângă premisa dată de oscilaţiile în cuadratură ale energiei giroscopice a Pământului, care sânt prezente în mod continuu, mai este necesară şi prezenţa altor factori care să conlucreze cu oscilaţiile în cuadratură.

Acelaşi tip de oscilaţii în cuadratură se obţin şi în relaţia gradientului energiei giroscopice.

3.4  Caracterul potenţial al câmpului vectorial grad e_g

Condiţia necesară şi suficientă ca un câmp vectorial să fie potenţial este ca rotorul acestuia să fie nul, [6], paragraful 110.

Rotorul câmpului vectorial format de gradientul energiei giroscopice a corpului material giroscopic, [3], [6], [7], se calculează cu expresia:

(40)

Conform relaţiei (40),

(41)

rotorul gradientului este nul, ceea ce confirmă că şi în cazul corpului material girocopic cu precesie, câmpul de forţă al gradientului energiei giroscopice totale este de tip potenţial.

Câmpul vectorial grad e_g fiind un câmp vectorial potenţial, în conformitate cu [7], paragraful 3.2.16, există o funcţie scalară de forma V = - e_g care reprezintă potenţialul scalar al vectorului grad e_g, dacă e_g are valori unice. Cum 

(42)

şi componentele sale au valori unice de-a lungul razelor r_z şi r_z1, rezultă că funcţia

 (43)

reprezintă potenţialul scalar al vectorului grad e_g.

4  Dependenţa energiei giroscopice de unghiul de nutaţie J

Energia giroscopică a corpului material giroscopic cu precesie şi gradientul acesteia au fost analizate în paragrafele precedente. În ambele analize, unghiul de nutaţie J a fost considerat cu valoarea în intervalul (0, p/2), dar, în realitate, valoarea unghiului este cuprinsă în intervalul [0, p].

Pentru a avea o imagine completă asupra dependenţei energiei giroscopice de unghiul de nutaţie J şi, implicit, a comportării gradientului, vom extinde analiza şi la valorile unghiului de nutaţie din afara intervalului considerat (0, p/2).

a) Unghiul de nutaţie J = 0

Aparent, deoarece pentru J = 0, relaţia (19) devine

(44)

în care vectorii  w şi w₁ sânt vectori coliniari, sântem tentaţi să considerăm că suma din paranteza relaţiei (43) ar reprezenta suma celor doi vectori, ceea ce nu este corect. Relaţia (43) arată că, în cazul   w₁ || w, , cele două viteze unghiulare de rotaţie acţionează independent şi acţiunile lor se însumează.

Cum cos(J = 0) = 1 şi sin(J = 0) = 0, coeficienţii k₁ şi k₂ din relaţiile (26) au valoarea zero. Aceasta înseamnă că dreptele x₁ = 0 şi x₂ = 0, coroborate cu condiţia y = 0, conduc la axa z de-a lungul căreia sânt dispuse valorile minime ale energiei giroscopice.

Pentru J = 0, gradientul energiei giroscopice, dat de relaţia (32), devine

(45)

adică este suma gradientelor energiilor giroscopice ale vitezelor de rotaţie w şi w₁, considerate separat.

Dreptele valorilor minime ale gradientului energiei giroscopice x₃ = 0 şi x₄ = 0, coroborate cu condiţia y = 0, de asemenea, conduc la axa z de-a lungul căreia gradientul energiei giroscopice are valori minime.

Parantezele din relaţiile (43) şi (44) prezintă o importanţă deosebită şi ne permit formularea următoarei teoreme:

Teorema 1:   Dacă două viteze de rotaţie w şi w₁ acţionează simultan asupra unui corp material, ambele imprimându-i o mişcare de rotaţie în jurul aceleiaşi axe, atunci energia giroscopică a corpului material este egală cu suma energiilor giroscopice produse de cele două viteze de rotaţie considerate separat, iar gradientul energiei giroscopice sumă este egal cu suma gradientelor energiilor componente.

 Conform acestei teoreme, un corp material giroscopic poate pierde sau câştiga energie prin vectori de rotaţie coliniari vectorului de rotaţie giroscopică.

b) Unghiul de nutaţie J = p/2

Cum sin(J = p/2) = 1 şi cos(J = p/2) = 0, relaţia (19) devine

(46)

iar gradientul energiei giroscopice, exprimat prin relaţia (32), devine

(47)

Coeficienţii dreptelor de valori minime ale energiei giroscopice, exprimaţi prin relaţiile (26), iau valorile k₁ = 0 şi 1/k₂ = 0, care conduc la condiţiile x = 0 şi, respectiv, z = 0. Aceste condiţii, coroborate cu condiţia y = 0, [a se vedea concluzia 5)], conduc la dreptele z şi, respectiv, x de-a lungul cărora sânt dispuse valorile minime ale energiei giroscopice.

Aceeaşi situaţie se prterece şi cu dreptele de valori minime ale gradientului energiei giroscopice. Valorile coeficienţilor k₃ = 0 şi 1/k₄ = 0, exprimaţi prin relaţiile (34), conduc la condiţiile x = 0 şi, respectiv, z = 0. Aceste condiţii, coroborate cu condiţia y = 0, [a se vedea relaţia (34)], conduc tot la dreptele z şi, respectiv, x de-a lungul cărora sânt dispuse şi valorile minime ale gradientului energiei giroscopice.

Prin urmare, în cazul J = p/2, dreptele de-a lungul cărora sânt dispuse valorile minime ale energiei giroscopice şi ale gradientului acesteia sânt drepte ortogonale suprapuse pe axele x şi z.

Relaţia (45) arată că, în cazul J = p/2, energia giroscopică a corpului material giroscopic cu precesie se compune din două mişcări giroscopice fără precesie faţă de axele ortogonale z şi x, cu vitezele de rotaţie ortogonale w şi, respectiv, w₁. Ca urmare, şi gradientul energiei giroscopice a corpului material giroscopic cu precesie se compune din gradientele celor două mişcări giroscopice fără precesie faţă de axele z şi x, cu vitezele de rotaţie ortogonale w şi, respectiv, w₁, ceea ce relevă şi relaţia (46).

În consecinţă, relaţiile (45) şi (46) permit formularea următoarei teoreme:

Teorema 2:    Dacă unghiul de nutaţie atinge valoarea J = p/2, atunci mişcarea giroscopică cu precesie a unui corp material giroscopic se descompune în două mişcări giroscopice simultane, ambele fără precesie, în jurul a  două axe ortogonale.

În acest caz, J = p/2, pe baza teoremelor 1 şi 2, se poate conchide:

Teorema 3:    Dacă unghiul de nutaţie J = p/2, atunci corpul material giroscopic poate primi sau pierde energie prin orice vector de rotaţie coliniar cu unul dintre vectorii de rotaţie ortogonali w sau w₁.  

Nota 4:  În subcapitolul 6.2 din [1], se demonstrează că planetele unui sistem planetar au mişcare giroscopică cu precesie, iar unghiul de nutaţie creşte pe măsura îndepărtării traiectoriei planetei de cele două focare ale sistemului. Faptul este confirmat practic de planetele sistemului nostru planetar format în jurul aştrilor Soarele şi Dacia. (A se vedea postările „Steaua dublă Soarele – Dacia” şi „Steaua dublă Soarele – Dacia, completare”, pe prezentul blog).

c) Unghiul de nutaţie p/2 < J < p

Dacă se notează J¢ = p - J, se obţine sinJ¢ = sinJ şi cosJ¢ = - cosJ, ceea ce conduce la schimbarea semnului termenilor care conţin pe cosJ în relaţiile energiei giroscopice (19) sau (20) şi în relaţiile gradientului (32) sau (33). Aceasta însemnă că mişcarea giroscopică cu precesie cu J Î (p/2, p), este aproximativ similară cu mişcarea giroscopică cu precesie cu J Î (0,p/2), cu inversare de sens.

În acest caz, este interesantă şi analiza dreptelor de valori minime ale energiei giroscopice şi ale gradientului acesteia. Atât coeficienţii k₁ şi k₂, daţi de relaţiile (26), cât şi coeficienţii k₃ şi k₄, daţi de relaţiile (34), schimbă semnul faţă de coeficienţii din cazul J Î (0, p/2).

Cu alte cuvinte, dreptele x₁ = k₁z, x₂ = k₂z, x₃ = k₃z, x₄ = k₄z,  din cazul J Î (0, p/2), se rotesc cu p/2, în cazul J Î (p/2, p). În primul caz, dreptele erau dispuse în cadranele I şi III ale planului x0z, în al doilea caz dreptele sânt dispuse în cadranele II şi IV ale aceluiaşi plan.

d) Unghiul de nutaţie J = p

Deoarece sinp = 0, cazul este identic cu cazul a) în care J = 0, vectorii w şi w₁fiind de sensuri contrare.

5  Mişcarea giroscopică cu precesie însoţită de o mişcare liniară

Spre deosebire de mişcarea giroscopică fără precesie însoţită de o mişcare liniară de viteză u, analizată în paragraful 2.2.5 din subcapitolul 2.2 din [1], mişcarea giroscopică cu precesie însoţită de o mişcare liniară de viteză u este mai complexă. Elementul de masă al corpului material giroscopic cu precesie care execută şi o mişcare liniară de viteză u este supus simultan la trei mişcări:

-        o mişcare de rotaţie giroscopică de viteză unghiulară w şi de viteză liniară v;

-        o mişcare de rotaţie de precesie de viteză unghiulară w₁ şi de viteză liniară v₁;

-        o mişcare de viteză u, care, la rândul ei, poate fi de rotaţie (cu viteza unghiulară w₁, conform analizei din paragraful 2.2.5 din [1]) sau o mişcare liniară simplă.

În [1] s-a demonstrat că sub acţiunea combinată a vitezelor liniare de rotaţie giroscopică v şi de precesie v₁, în corpul material giroscopic cu precesie se creează tensiuni interne, maximul şi minimul acestora fiind dispuse pe o secţiune diametrală verticală care conţine axa z. Cauza acestor tensiuni este mişcarea de rotaţie de precesie.

Într-un corp material giroscopic solid, tensiunile interne provoacă crăpături în scoarţa acestuia, iar dacă scoarţa pluteşte pe fluid, se produc deplasări ale plăcilor scoarţei. Într-un corp material giroscopic gazos, tensiunile interne produc regruparea masei acestuia, sub formă de spirale. 

Dacă se adăugă vitezelor liniare de rotaţie v şi v₁ şi o mişcarea liniară de viteză u, care este o mişcare de rotaţie în jurul unui corp central, atunci tensiunile interne din corpul material giroscopic cu precesie se amplifică, fricţiunile dintre plăci şi deplasările acestora se măresc sau se conturează mai clar spiralele, în funcţie de natura corpului.

În cazul în care mişcarea liniară de viteză u nu reprezintă o mişcare în jurul unui corp central, mărimea tensiunilor interne creşte şi creşte şi numărul axelor acestora, în funcţie de mărimea şi variaţia vitezei liniare u, care, la rândul ei, poate fi suma mai multor viteze liniare ce acţionează simultan asupra corpului material giroscopic.

Bibliografia

1  CONSTANTIN TEODORESCU: Structură şi evoluţie. Editura MATRIX ROM.

    Bucureşti 2016. Ediţia a 5 – a revizuită şi adăugită.

2  GABRIELA ŢIŢEICA şi ALEXANDRU STOENESCU: Teoria giroscopului şi aplicaţiile sale tehnice. Tipografia Curţii Regale F. GÖBL FII S.A. Bucureşti, 1945.

3  MIRCEA DRĂGANU: Introducere matematică în fizica teoretică modernă. Vol. 1. Editura tehnică, Bucureşti, 1957.

4  ION DIMA (coordonator): Dicţionar de fizică. Editura enciclopedică română, Bucureşti, 1972.

5  V. I. SMIRNOV: Kurs vâsşei matematiki. Tom pervâi. Gosudarstveno izdatelstvo tehniko – teoreticeskoi literaturî. Moskva, 1953.

6  V. I. SMIRNOV: Kurs vâsşei matematiki. Tom vtoroi. Gosudarstveno izdatelstvo tehniko – teoreticeskoi literaturî.  Moskva, 1953.

7   ANDRE ANGO: Matematika dlia electro - i radioinjenerov. Perevod s franţuscovo (André ANGOT) Izdatelstvo “Nauka”. Glavnaia redakţia fizico – Matematiceskoi literaturî. Moscva, 1967.