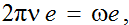Căldura şi procesele termice - teorie nouă (III)

Autor: ing. Constantin Teodorescu

Articolul "Căldura şi procesele termice - teorie nouă (III)" explică evoluţiile termice în spaţiul galactic, în cadrul noii teorii a căldurii şi proceselor termice, elaborată pe baza concepţiei şi legilor fundamentale universale demonstrate în studiul "Structură şi evoluţie" al autorului

Cuprins:

1  Formarea de atomi grei prin răcire excesivă

2  Formarea elementelor prin răcirea plasmei

3  Plasma în Univers

III  Evoluţii termice în spaţiul galactic

Mai întâi să observăm că desfăşurarea proceselor termice nu are acelaşi caracter de-a lungul tuturor etapelor înşirate pe figura 1 din postarea (II). Dacă de-a lungul celor trei stări de agregare (solidă, lichidă, gazoasă), evoluţia proceselor este lină şi reversibilă, deja din etapa atomilor izolaţi evoluţia îşi pierde treptat caracterul lin şi reversibil şi devine violentă. Iar în etapele formării de atomi grei, plasmei de protoni şi neutroni şi plasmei de electroni, evoluţia este pur violentă, bazată pe ciocniri.

Pe scurt, vom analiza şi aspectele referitoare la etapele violente.

1   Formarea de atomi grei prin răcire excesivă

Prin răcire, molecula pierde energie, iar pierderea de energie se manifestă prin micşorarea vitezei unghiulare de rotaţie, w_n, a mişcării de rotaţie giroscopică sincronă şi unitară a nucleelor şi structurilor de energie din jurul acestora, conform relaţiei (1) din (I). 

Așa cum s-a arătat în analiza stării solide a moleculei, prin micşorarea vitezei unghiulare de rotaţie w_n, se lărgeşte zona de întrepătrundere a structurilor de energie din jurul nucleelor.

Când viteza unghiulară de rotaţie w_n atinge limita inferioară a stării solide, adică la realizarea egalităţii w_n = w_{n, s}, unghiul de întrepătrundere al structurilor de energie din jurul nucleelor devine maxim, de 120^o în planul ecuatorial al moleculei, iar distanţa dintre nucleele moleculei devine egală cu raza r_a a structurilor de energie din jurul nucleelor, conform realţiei (16) din (I). La atingerea valorii w_n = w_{n, s} a vitezei unghiulare de rotaţie a nucleelor şi structurilor de energie din jurul lor, se atinge de fapt limita de stabilitate a moleculei în stare solidă, care este dată de realizarea egalităţii dintre forţele centrifuge F_ce ale structurilor de energie, determinate de relaţia (1) din (I), şi forţele de atracţie F_am dintre masele nucleelor, determinate de relaţia (10) din (I), adică F_ce = F_am. Această egalitate, în (I) a fost scrisă sub forma

      (49)

în care r_a este raza atomului sau raza structurii de energie, a_s este semidistanţa dintre nuclee, F_c este forţa centrifugă la distanţa a_s de axa de rotaţie şi, corespunzător, la distanța r_a de axa de rotație, iar F_am este forţa de atracţie dintre masele nucleelor la distanţa 2a_s dintre nuclee.

Conform relaţiilor (1) din (I), pentru forţa centrifugă, şi (9.65) din [1], pentru forţa de atracţie a maselor nucleelor, în planul ecuatorial al moleculei, z = 0, relaţia (49) capătă forma 

     (50)

în care E_r este energia de rotaţie în structurile de energie, iar m_n este masa nucleului și nucleele au fost considerate identice.

Răcirea în continuare a moleculei, adică scăderea energiilor rotaţiilor giroscopice ale nucleelor şi structurilor de energie din jurul lor, atrage după sine şi scăderea vitezei unghiulare de rotaţie w_n a acestora sub valoarea w_{n, s}, corespunzătoare limitei stării solide a moleculei, deoarece atât energia giroscopică a elementului de masă din nucleu, e_g = m(w_nr_z)²/2 conform relaţiei (2.2.3) din [1], cât şi energia de rotaţie a structurilor de energie, E_r = ew_n conform relaţiei (1) din (I), sânt direct proporţionale cu w_n.

 Iar inegalitatea w_n < w_{n, s} transformă şi egalitatea F_ce = F_am, corespunzătoare egalităţii w_n = w_{n, s}, în inegalitatea F_ce < F_am, deoarece masele nucleelor au rămas nemodificate, rămânând nemodificate şi forţele de atracţie dintre masele lor F_am.

Apariţia inegalităţii F_ce < F_am înseamnă stricarea echilibrului de forţe ce acţionează între cele două nuclee ale moleculei şi, sub influenţa forţelor de atracţie dintre masele lor, cele două nuclee ale moleculei încep să se apropie unul de altul.

Mişcarea de apropiere a nucleelor şi contactul dintre ele se pot produce în două feluri:

-        lent sau

-        brusc.

Apropierea lentă se produce când răcirea moleculei se continuă lent şi se soldează cu contopirea celor doi atomi ai moleculei şi transformarea moleculei într-un atom de două ori mai greu.

Ciocnirea între două particule identice, doi electroni, ambele cu mişcări giroscopice identice şi cu vectorii vitezelor unghiulare de rotaţie paraleli şi de acelaşi sens, numită ciocnire tip sfârlează sau elice, a fost analizată şi descrisă în capitolul 7 subparagraful 7.5.2.1 şi ilustrată pe figura 7.7 din [1]. Cum ambele nuclee din moleculă sânt identice ca structură, au vitezele unghiulare de rotaţie identice, paralele şi de acelaşi sens, există tentaţia de a considera şi ciocnirea lor de tipul sfârlează sau elice. Apare însă un impediment.

Electronii consideraţi în ciocnirea tip sfârlează sau elice sânt particule identice, dar sânt şi particule simetrice şi de formă sferică. Ori nucleele din molecule sânt structuri asimetrice şi cu mişcări giroscopice. Ca atare, ciocnirea nucleelor din molecule nu poate fi tratată  ca fiind de tipul sfârlează sau elice.

Înainte de a ne lămuri cu privire la ciocnirea nucleelor din moleculă, să menţionăm că sânt şi nuclee cu structuri simetrice şi acestea sânt nucleele elementelor din grupa gazelor rare (heliu, neon, argon şi altele) care, tocmai din această cauză, sânt şi elemente monoatomice.

Spre deosebire de nucleele elementelor din grupa gazelor rare, care fiind simetrice le împiedică atât să formeze molecule cât şi să reacţioneze chimic cu alte elemente, nucleele celorlalte elemente fiind nesimetrice sânt apte pentru o largă varietate de reacţii chimice.  

Prin urmare, în toate moelculele, nucleele nefiind simetrice şi aflate în mişcări giroscopice sincrone, prin ciocnire nu se alipesc unul de altul ci se recompun, se reconfigurează într-un singur nucleu de două ori mai greu şi cu aceeaşi viteză unghiulară de rotaţie giroscopică pe care au avut-o în momentul ciocnirii.

Structurile de energie din jurul celor două nuclee, pe măsură ce nucleele se apropie unul de altul, se întrepătrund din ce în ce mai mult şi, în momentul ciocnirii şi reconfigurării nucleelor, se contopesc într-o singură structură de energie ce se roteşte în jurul nucleului nou format, sincron cu rotaţia giroscopică a acestuia. S-a format astfel atomul unui element de două ori mai greu.

La o răcire bruscă a moleculei şi ciocnirea nucleelor va fi bruscă şi există şansa ca, în loc să se formeze un atom de două ori mai greu, molecula să explodeze prin dezintegrarea nucleelor.

Fenomenele descrise mai sus pot fi produse şi artificial în laborator, dar se produc şi în mod natural. Producerea artificială nu trebuie confundată cu activitatea alchimiştilor, fiindcă aceştia urmăreau transformarea elementelor pe cale chimică, ceea ce e irealizabil. Pe cale chimică pot fi transformate molecule, prin contopire sau adaos de atomi, dar nu poate fi obţinut un element nou. Calea lentă descrisă mai sus este altceva decât alchimia.

Laboratorul enorm în care se produce transformarea moleculelor în atomi de elemente mai grele este spaţiul interstelar din interiorul galaxiilor şi spaţiul intergalactic, care sânt spaţii excesiv de reci. Dovada acestei transformări ne este oferită de compoziţia meteoriţilor căzuţi pe Pământ, care conţin cantităţi mari de elemente grele.

2   Formarea elementelor prin răcirea plasmei

Evident că mai înainte de a răci plasma, trebuie să arătăm unde există plasmă în cosmos. Deocamdată s-au identificat două locuri: în „stele” şi în jeturile care „sânt aruncate” din „găurile negre” din centrul galaxiilor. Am folosit ghilimele pentru unii termeni pentru că vom vedea că înţelegerea lor actuală nu concordă cu realitatea.

Mai întâi „stelele” sânt considerate corpuri cereşti aflate în stare de incandescenţă care evoluează spre un „deznodământ exploziv”, datorită unor „procese nucleare” ce se produc în interiorul lor. Totodată, în jurul unora dintre stele orbitează, împreună, alte corpuri cereşti dintre care unele sânt reci iar altele aproape incandescente, cum sânt planetele din jurul Soarelui. Iată deja o contradicţie: evoluţii diferite ale unor corpuri cereşti aflate în aceleaşi condiţii de răcire ale spaţiului galactic în care se află, spaţiul dintre corpuri fiind extrem de rece. Cum toate corpurile din Univers se află sub influenţa legii atracţiei dintre energia câmpului universal şi propriile energii, corpurile cereşti din aceeaşi zonă galactică se află în acelaşi regim termic de răcire sau de încălzire caracteristic zonei. Aceasta înseamnă că Soarele se află în acelaşi proces de răcire cu planetele ce orbitează în jurul său, caracteristic locului pe care îl ocupă în Galaxie.

Faptul că şi stelele se răcesc fără a „exploda” datorită unor „procese nucleare” din interiorul lor este dovedit şi de existenţa stelei Dacia cu care Soarele formează o stea dublă, conform demonstraţiei din subcapitolul 6.2 din [1]. Faptul că o stea cu masa mult mai mare decât a Soarelui şi situată doar la 60 UA depărtare nu este văzută se datorează emisiei slabe de lumină pe care o are, ca urmare a stării reci la care a evoluat.

Asta înseamnă că stelele pe care le observăm în cadrul Galaxiei sânt doar cele care emit suficientă lumină ca să fie văzute, dar că printre ele, cu aceeaşi mişcare de rotaţie în jurul axei Galaxiei, roiesc şi puzderie de stele reci ce nu se văd. Cum masa acestor aştri neobservabili este pusă în evidenţă de calculele făcute de astronomi în cercetarea diferitelor fenomene cosmice, s-a inventat noţiunea de „materie neagră” care ar coexista împreună şi printre materia din Galaxie. Dar nu e vorba de „materie neagră” ci e vorba de stele reci neobservabile, ajunse în stare rece datorită procesului general de răcire în care se află Galaxia.

Desigur se va obiecta că totuşi explozii stelare s-au observat. Da, este adevărat, au fost şi vor mai fi explozii accidentale produse prin ciocnirea a două corpuri sub forţa atracţiei dintre masele lor, aşa cum se întâmplă la căderea unor meteoriţi mai mari sau, Doamne fereşte, cum s-ar întâmpla la căderea unui asteroid. În capitolul 9, în subparagraful 9.4.2 din [1], a şi fost demonstrat caracterul distructiv al impactului mişcării gravitaţionale, acesta fiind şi titlul subparagrafului.

Aşadar, Galaxia se află în proces de răcire, iar stelele din interiorul ei se află în etape diferite ale procesului de răcire, acoperind practic toată plaja de etape prezentate pe fig. 1 din (I).

Acum însă ne interesează formarea elementelor în plasma aflată în răcire din stelele observabile ale Galaxiei, inclusiv Soarele.

Formarea protonilor şi neutronilor prin ciocnirea plastică a electronilor aflaţi în mişcare giroscopică în plasma fierbinte a fost demonstrată în capitolul 7, în paragrafele 7.6 şi 7.7 din [1]. De asemenea, în capitolul 8, în paragraful 8.3 „Atomul” din [1], a fost demonstrată formarea atomilor celor mai uşoare elemente.

Aspectul esenţial în formarea elementelor îl constituie formarea nucleelor, deoarece completarea structurii de electroni ce vor orbita în jurul nucleului format este relativ simplă şi se realizează rapid din norul de electroni aflat în plasma în răcire.

Cel mai simplu atom, cel de hidrogen, constă dintr-un nucleu în jurul căruia orbitează un electron, iar nucleul este format dintr-un singur proton la atomul simplu sau dintr-un proton şi unul sau doi neutroni la atomii izotopilor, ca în figura 2, a).

Figura 2. Formarea nucleelor din protoni (p) şi neutroni (n).

Din nucleul celui mai greu izotop al hidrogenului, prin captarea încă a unui proton, se formează nucleul de heliu, figura 11.13, b). Nucleul de heliu este foarte stabil şi este primul dintre gazele rare.

Pe baza nucleului de heliu, foarte stabil, se formează succesiv nucleele elementelor din perioada a doua a tabelului lui Mendeleev.     

Din nucleul de heliu, prin captarea a încă doi neutroni şi un proton, se formează nucleul de litiu, figura 11.13 c). Din nucleul de litiu, prin captarea a încă un neutron şi un proton, se formează nucleul de beriliu, figura 11.13 d). Şi tot aşa, prin captări succesive de neutroni şi protoni, se formează pe rând nucleele de bor, carbon, azot, oxigen şi fluor. Din nucleul de fluor, care are 9 protoni şi 10 neutroni, prin captarea a încă unui proton, se formează nucleul de neon, figura 11.13 e). 

Pe baza nucleului de neon, al doilea element din grupa gazelor rare şi, la fel ca heliul, foarte stabil, se formează succesiv nucleele elementelor din perioada a treia a tabelului lui Mendeleev: sodiu, magneziu, aluminiu, siliciu, fosfor, sulf şi clor, ultimul cu 17 protoni şi 19 neutroni. Din nucleul de clor, prin captarea a încă trei neutroni şi un proton, se formează nucleul de argon, figura 11.13 f), cu 18 protoni şi 22 neutroni, al treilea element din grupa gazelor rare, de asemenea foarte stabil.

În acelaşi fel continuă formarea elementelor din perioadele următoare, dar apar unele diferenţe. Dacă între heliu şi neon, în perioada a 2-a, şi între neon şi argon, în perioada a 3-a, sânt câte 7 elemente, între argon şi kripton, în perioada a 4-a, şi între kripton şi xenon, în perioada a 5-a, sânt câte 17 elemente, între xenon şi radon, în perioada a 6-a, sânt 31 de elemente, iar după radon mai sânt, în perioada a 7-a, încă 19 elemente, dar fără a se mai ajunge la un gaz rar.

Tot acest tablou al nucleelor elementelor evidenţiază, pe de o parte, că nucleele sânt de două tipuri:

-        asimetrice şi

-        simetrice

şi, pe de altă parte, că proprietăţile elementelor depind de simetria nucleelor lor.

Observăm, mai întâi, că toate elementele din grupa gazelor rare, grupa a 8-a, (heliu, neon, argon, kripton, xenon şi radon) au nucleele perfect simetrice şi din această simetrie perfectă rezultă atât marea lor stabilitate şi lipsa de afinitate chimică, adică lipsa capacităţii de a reacţiona chimic cu alte elemente, cât şi faptul că toate sânt elemente monoatomice, atomii lor neunindu-se în molecule.

În schimb, toate elementele cu nucleele asimetrice dovedesc atât o mare afinitate chimică, adică au o mare capacitate de a reacţiona chimic cu alte elemente, cât şi faptul că sânt elemente moleculare, atomii lor unindu-se în molecule.

Am depistat astfel principala cauză a unirii atomilor în molecule: asimetria nucleelor. Într-adevăr, asimetria nucleelor face ca mişcarea lor giroscopică să devină o mişcare giroscopică cu precesie, adică simultan cu rotirea în jurul propriei axe cu viteza unghiulară w_n a nucleului, axa sa de rotaţie 0z execută şi ea o roataţie în jurul unei alte axe 0z₁, numită axă de precesie, cu viteza de rotaţie unghiulară w_n1. Unghiul de nutaţie J dintre axele 0z şi 0z₁ este determinat de gradul de asimetrie al nucleului. (Pentru a înţelege caracteristicile mişcării giroscopice cu precesie, a se revedea subcapitolul 2.3 din [1], în care este analizată).

Mişcarea giroscopică cu precesie a nucleelor asimetrice provoacă instabilitatea atomilor, astfel că atomii sânt obligaţi să caute o stare mai stabilă fie prin unirea cu un alt atom similar fie cu un atom de alt element, formând o moleculă.

În cazul moleculei formată din doi atomi, identici sau diferiţi, mişcările de rotaţie ale celor două nuclee şi ale structurilor de energie din jurul lor se sincronizează într-o mişcare comună cu axele de rotaţie A₁z şi A₂z paralele şi cu structurile de energie din jurul nucleelor cu acelaşi plan ecuatorial, A₁ şi A₂ find centrele atomilor uniţi în moleculă. Totodată, mişcarea giroscopică sincronizată a celor două nuclee împreună cu structurile de energie din jurul lor, execută şi o mişcare de rotaţie în jurul axei de precesie 0z₁ care, prin unirea atomilor în moleculă a devenit una singură şi s-a plasat în centrul moleculei. Astfel, întreaga moleculă execută aceeaşi mişcare de precesie, sincron şi unitar şi dovedind mai multă stabilitate.

Marea instabilitate a atomilor singulari cu nuclee asimetrice şi uşoara instabilitate şi a moleculelor formate de aceştia sânt cauzele afinităţii lor chimice, a capacităţii de a reacţiona chimic şi de a forma molecule complexe, în tendinţa de a anihila precesia mişcărilor lor giroscopice.

Să mai menţionăm că procesele de formare a nucleelor şi atomilor sânt caracteristice etapei plasmei de protoni şi neutroni, îndeosebi a atomilor uşori şi semigrei, dar şi etapei de formare de atomi grei a excesivei răciri, conform figurii 1 din (I).

În schimb, afinitatea chimică, capacitatea de a reacţiona chimic, este caracteristică etapei atomilor izolaţi şi îndeosebi etapelor celor trei stări de agregare: gazoasă, lichidă şi solidă, conform figurii 1 din (I).      

3   Plasma în Univers

Am analizat evoluţia structurilor atomice şi moleculare de-a lungul tuturor etapelor proceselor reversibile de încălzire şi de răcire, cu excepţia etapei plasmei de electroni şi ne propunem să prezentăm câteva aspecte şi ale acestei etape.

Oricât de fierbinţi ar fi stelele, plasma din ele nu conţine numai electroni ci şi protoni şi neutroni. Plasma care să conţină numai electroni se găseşte numai în jeturile de energie şi de masă pe care găurile lipsite de energie sau aşa-numitele găuri negre, aflate în centrul galaxiilor, le absorb din spaţiul cosmic, cu o forţă incredibilă, ca în figura 3.

Figura 3. Jeturile de plasmă absorbite de galaxie prin pâlniile găurii lipsite de energie,

care mai este numită şi gaură neagră..

Existenţa jeturilor de energie care ţâşnesc din găurile negre din centrul galaxiilor este dovedită de observaţiile astronomice din ultima vreme şi s-au obţinut excelente fotografii ale acestora. Aşa că existenţa lor nu mai poate fi pusă la îndoială. Este neveridică însă explicaţia care li s-a dat. Savanţii contemporani, bazându-se pe teoria generalizată a relativităţii a lui Einstein, interpretează găurile negre ca singularităţi ale curburii gravitaţionale spaţiu – timp în care sânt concentrate mase enorme. Iar din aceaste mase enorme, pe baza unor procese interne, pe care însă nu le explică, ţâşnesc aceste jeturi de plasmă cu o viteză comparabilă cu a luminii.

În studiul [1], în capitolul 5, existenţa găurilor negre, care de fapt sânt găuri lipsite de energie, a fost dovedită pe baza legilor fundamentale ale Universului.

La intersecţia a două forţe de atracţie cu direcţii diferite, produse de două structuri de energie existente în câmpul universal de energie, elementele de energie din zona intersecţiei, sub influenţa forţelor de atracţie ce se intersectează, încep a se mişca curbiliniu. La apariţia mişcării curbilinii a elementelor de energie, câmpul universal de energie acţionează prin forţa sa de atracţie şi, de-a lungul razei de curbură a mişcării curbilinii apare forţa centrifugă ce tinde să împrăştie elementele de energie aflate în mişcare curbilinie.

Forţa centrifugă, pentru a împrăştia energia ce se mişcă curbiliniu, acţionează în două feluri:

-        direct asupra energiei ce se mişcă curbiliniu, pe direcţia razei de curbură,

-        dar şi de-a lungul razei de curbură.

Conform relaţiei (5.7) din capitolul 5 din [1], forţa centrifugă este direct proporţională cu elementul de energie e asupra căruia acţionează şi invers proporţională cu raza de rotaţie r_z, adică F_ce = e/r_z, relaţie conformă cu legea fundamentală a mişcării demonstrată în paragraful 9.4 din capitolul 9 tot din [1]. Prin urmare, forţa centrifugă creşte pe măsura apropierii de centrul curburii mişcării curbilinii, iar în centrul tinde către infinit. Iată cum apare primul semn al existenţei unei găuri lipsite de energie chiar în centrul mişcării curbilinii. În locul energiei împinsă de forţa centrifugă în lungul razei de curbură, în centrul mişcării curbilinii năvăleşte energie din afara planului mişcării curbilinii, energie care este şi ea împinsă de-a lungul razei de curbură de forţa centrifugă. Astfel se stabileşte un curent de energie în lungul razei de curbură care presează energia aflată în mişcare curbilinie să se disperseze, dar energia dispersată este imediat înlocuită de forţele ce se intersectează dacă acestea persistă a fi prezente.

La persistenţa forţelor ce se intersectează, mişcarea curbilinie de energie se închide şi devine o mişcare de-a lungul unui contur închis. În această situaţie, energia aflată în mişcare în lungul conturului închis, conform legii universale a atracţiei dintre energii, creează propria forţă de atracţie cu care acţionează atât asupra energiei aflată în mişcare curbilinie cât şi asupra energiei din afara acesteia.

În capitolul 5 din [1], s-a demonstrat că forţa de atracţie a mişcării aflată în mişcare curbilinie are două componente cu roluri diferite:

-         o componentă în planul mişcării curbilinii, numită componenta orizontală, care este egală şi de sens contrar forţei centrifuge, şi

-         o componentă perpendiculară pe planul mişcării curbilinii, numită componenta verticală.

La rândul ei, componenta orizontală a forţei de atracţie a energiei în mişcare curbilinie are două efecte:

a)      Fiind egală şi de sens contrar forţei centrifuge, întrerupe curentul de energie din lungul razei de curbură, stabilizând energia de mişcare curbilinie.

b)     Transformă mişcarea curbilinie într-o mişcare de rotaţie în jurul aceleaşi axe de rotaţie şi cu raza de rotaţie constantă.

După cum s-a demonstrat în paragrafele 5.5 şi 5.6 din capitolul 5 din [1], energia giroscopică a elementului de energie e aflat în mişcare de rotaţie circulară este determinată şi de poziţia sa faţă de planul orizontal: dacă în planul orizontal e_g(e) = e, în afara planului orizontal depinde şi de coordonata z, adică e_g(e) = e(z + 1), conform relaţiei (5.64).

Prin transformarea mișcării curbilinii în mișcare circulară de rotație, în expresiile forței centrifuge şi forţei de atracţie trebuie luată în calcul energia giroscopică a elementului de energie e. Conform relaţiei (5.67) din [1], forţa centrifugă a energiei în mișcare de rotație are expresia

    (51)

Forţa de atracţie a energiei în mişcare de rotaţie, conform relaţiei (5.76) din [1], are expresia

     (52)

Comparând relațiile (51) și (52), e uşor de observat că forţa de atracţie are variaţia în funcţie de unghiul q diferită de forţa centrifugă. Dacă pentru q = p/2 forţa de atracţie şi forţa centrifugă sânt egale, pentruq tinde către zero ambele forțe tind către infinit, dar forța de atracție are creşterea mult mai puternică.  

La acest stadiu al demonstrației, apare tentația de a considera lămurită cauza jeturilor de energie ca fiind forţa de atracţie ce tinde spre infinit în apropierea axei de rotaţie. Dar să nu ne grăbim pentru că nu avem încă explicată gaura lipsită de energie, deoarece în planul ecuatorial (orizontal) al energiei în rotaţie circulară aceasta s-a redus la un singur punct, prin compensarea forţei centrifuge de către componenta orizontală a forţei de atracţie.

În subparagraful 5.6.3 din capitolul 5 din [1], prin analiza potenţialului vectorial al forţei de atracţie, s-a demonstrat că rotorul acesteia este coliniar şi de sens opus rotorului forţei centrifuge. Rotorul rezultant al diferenţei celor doi rotori coliniari, relaţia (5.106) din [1], este de forma

     (53)

şi are valoarea zero în planul ecuatorial şi creşte parabolic în funcţie de z, după o curbă de gradul doi.  

Rotorul rezultant este perpendicular pe planul meridian (r, r_z) şi produce o mişcare de rotaţie în acest plan, caracterizată de relaţia (2.2.42) din subcapitolul 2.2 din [1], rot v = 2 w,  şi conform căreia 

      (54)

unde   reprezintă vitezele de rotaţie liniară şi unghiulară, în planul meridian (r, r_z).

Mişcarea circulară din planul meridian (r, r_z) produce o forţă centrifugă exprimată prin relația (5.112) din capitolul 5 din [1], de forma

       (55)

Forţa centrifugă manifestată în planul (r, r_z) are următoarele caracteristici:

-         în vecinătatea axei z, valoarea forţei tinde către infinit  

-         în plan meridional, creşte odată cu creşterea coordonatei z, proporţional cu funcţia z(z+1);

-         este o forţă care se manifestă puternic doar în vecinătatea şi apropierea axei z, este o forţă regresivă de acţiune apropiată, nu îndepărtată.

Prin urmare, forţa centrifugă  manifestată în planul (r, r_z), este forţa care generează gaura circulară din jurul axei z, în formă de clepsidră. 

 Să admitem că energia giroscopică e_g(e) se află pe raza r_z, la coordonata z şi la distanţa r_z de axa z. Concomitent cu mişcarea sa circulară orizontală, în plan paralel cu ecuatorul (x, y) şi situat la cota z, energia giroscopică este supusă şi mişcării circulare în planul (r, r_z), de către vectorul rotorul rezultant rot (F_ae, F_ce), conform raţionamentului de mai sus.

Deci, în preajma axei z, energia giroscopică este supusă simultan la două mişcări de rotaţie circulare, în planuri ortogonale: una în planul orizontal, în jurul axei z, şi una în planul vertical, în jurul unei axe proprii.

Forţa centrifugă produsă de mişcarea circulară din planul orizontal, planul paralel cu planul ecuatorial (x, y), este anihilată de componenta orizontală a forţei de atracţie, după cum s-a arătat mai sus. În schimb, forţa centrifugă produsă de mişcarea circulară din planul (r, r_z) nu este anihilată şi, împreună cu viteza de rotaţie liniară în planul meridian  imprimă energiei giroscopice e_g(e), o mişcare direcţionată în sus (spre creşterea coordonatei z) şi spre exteriorul structurii de energie, adică în sensul îndepărtării de axa z, figura 5.5, a), din capitolul 5 din [1]).

Odată cu deplasarea în sus, creşterea coordonatei z produce creşterea forţei centrifuge, relaţia (55), corespunzătoare creşterii funcţiei z(z + 1).

Creşterea forţei centrifuge împinge energia giroscopică e_g(e) mai sus, spre o crştere şi mai mare, şi mai spre exterior, îndepărtând-o tot mai mult de axa z. Această mişcare spre sus şi spre exterior se aplică, simultan, tuturor energiilor giroscopice aflate în vecinătatea axei z, în funcţie de poziţiile lor (în funcţie de z şi de r_z), şi rezultatul acestor mişcări simultane este crearea unui front de mişcare dinspre axa z. 

Prin creşterea distanţei faţă de axa z, creşterea lui r_z, forţa centrifugă scade puternic, invers proporţional cu cubul acesteia, relaţia (55), astfel că, la o anumită distanţă, îndepărtarea energiei giroscopice e_g(e) de axa z se opreşte.

Astfel, se obţine un spaţiu în jurul axei z, în care nu se află energie giroscopică, deoarece toată energia a fost împinsă în afara acestuia. Acest spaţiu are o formă circulară, cu raza crescătoare odată cu creşterea coordonatei z, creştere corespunzătoare funcţiei z(z + 1).

Deoarece fenomenul se produce asemănător şi simetric de-a lungul axei z, atât pentru z > 0 cât şi pentru z < 0, gaura din jurul axei z are forma de clepsidră, ca în figura 5.5, b) din capitolul 5 din [1]. Gaura din jurul axei z este mărginită de o parabolă de rotaţie în jurul axei z, în plan vertical, iar în planul ecuatorial, z = 0, are un mic orificiu, în jurul axei z. 

Datorită caracterului cumulativ al energiei giroscopice e_g(e), raza r_zc a găurii în formă de clepsidră, din jurul axei z, se modifică continuu, corespunzător cu evoluţia structurii de energie.

Mai trebuie menţionat faptul că, în afara găurii în formă de clepsidră din jurul axei z, acţiunea vectorului rotorului rezultant rot (F_ae, F_ce) se micşorează treptat şi contribuie la configurarea formei structurii de energie în imediata vecinătate a clepsidrei şi îşi pierde orice influenţă în spaţiul mai îndepărtat de clepsidră, devenind nesemnificativă.

Conform relaţiei (52), forţa de atracţie a energiei tinde către infinit în zona centrală a găurii lipsite de energie în formă de clepsidră, în jurul axei de rotaţie, şi este cea care absoarbe energie şi masă din spaţiul înconjurător, sub forma de jeturi ca în figura 3. Datorită forţei colosale cu care sânt atrase, energia şi masa absorbite se află în stare de plasmă foarte fierbinte, fiind formată numai din fotoni şi electroni.

Energia şi masa absorbite din spaţiul înconjurător sânt expulzate din clepsidra care le-a absorbit în interiorul structurii de energie cu mişcare giroscopică, fiind sursa de alimentare cu energie a acesteia. Evoluţia structurii de energie este în funcţie de evoluţia absorbţiei de energie prin jeturile clepsidrei.

Am demonstrat astfel nu numai că jeturile observate de astronomi nu sânt de expulzare ci de absorbţie, dar am descris şi procesul de formare a unei structuri de energie cu mişcare giroscopică. Procesul este acelaşi atât pentru vârtejul ce se formează pe câmp sau la colţul străzii cât şi pentru tornadă, ciclon tropical sau galaxie. Diferenţa constă în durata existenţei forţelor ce le crează: câteva secunde la vârtej, câteva minute sau zeci de minute la tornadă, câteva zile la ciclonul tropical şi o veşnicie relativă la galaxie, în comparaţie cu celelalte dar şi ea trecătoare în evoluţia Universului.   

Având în vedere analogia dintre ciclonul tropical şi galaxie, ambele având la bază o structură de energie cu mişcare giroscopică, există posibilitatea de a înţelege multe aspecte din evoluţia galaxiilor şi din mecanismele lor interne prin studierea sistematică a ciclonului tropical. Asemenea studii costă şi mai puţin şi sânt mai accesibile, deoarece nu necesită ieşiri în spaţiul cosmic, cicloanele tropicale fiind prezente anual în oceanele Atlantic şi Pacific.

Bibliografia

1  CONSTANTIN TEODORESCU: Structură şi evoluţie. Editura MATRIX ROM. Bucureşti 2016. Ediţia a 5 – a revizuită şi adăugită.

Căldura şi procesele termice - teorie nouă (II)

Autor: ing. Constantin Teodorescu

Articolul "Căldura şi procesele termice - teorie nouă (II)" explică emisia de energie în molecule şi atomi, în cadrul noii teorii a căldurii şi proceselor termice, elaborată pe baza concepţiei şi legilor fundamentale universale demonstrate în studiul "Structură şi evoluţie" al autorului.

II Emisia de energie în molecule şi atomi

Aşa cum s-a arătat în prima parte a subsubparagrafului 11.7.6.1 din [1], atât prin atomii constituiţi în molecule cât şi prin atomii separaţi, curge continuu energie.

Cu privire la scurgerea de energie din molecule şi atomi în mediul înconjurător, trebuie avute în vedere câteva aspecte.

Primul aspect este acela că din mediul exterior, energia pătrunde în moleculă sau în atom prin capetele găurilor lipsite de energie din jurul axelor de rotaţie ale nucleelor, străbate nucleele şi structurile de energie din jurul acestora, alimentând mişcarea lor giroscopică, şi surplusul iese înapoi în mediul exterior, prin extremităţile planelor ecuatoriale ale structurilor de energie. Astfel sânt realizate circuite permanente de energie care se menţin pe toată durata existenţei moleculelor şi atomilor. De bilanţul momentan al circuitelor de energie depinde caracterul de încălzire sau de răcire al proceselor pe care moleculele şi atomii le parcurg de-a lungul existenţei lor.

Al doilea aspect constă în faptul că electronii din interiorul moleculelor şi atomilor, mişcându-se pe traiectoriile orbitale în jurul nucleelor, se află permanent în interiorul structurilor de energie şi schimbă energie numai cu acestea, neavând contact direct cu mediul exterior. 

Al treilea aspect constă în caracterul ciclic al structurilor de energie ce se rotesc sincron cu mişcarea giroscopică a nucleelor, cu aceeaşi constantă ciclică k = 2pe, e fiind stropul elementar de energie definit şi determinat în paragraful 5.10 „Fotonul – structura elementară (fundamentală) de energie” din [1].

Caracterul ciclic al structurilor de energie se impune şi în schimbul de energie al acestora cu mediul exterior. Ca urmare, schimbul de energie dintre structurile de energie şi mediul exterior se realizează în două feluri diferite:

a)      prin emisie continuă de stropi elementari de energie e şi

b)     prin emisie de cuante de energie corespunzătoare constantei ciclice k.

Emisia continuă de stropi de energie este simţită de fiecare dintre noi în preajma unui corp încins sau îngheţat. Emisia de cuante de energie ne-a surprins când pentru prima dată după naştere am deschis ochii şi ne încântă în permanenţă dezvăluindu-ne frumuseţea lumii în care trăim. 

Cuanta de energie 2pe repetată de n ori pe secundă ne dă       

     (43)

emisia de fotoni de frecvența n = w / 2p .

Astfel de fotoni sânt emişi de molecule şi atomi de-a lungul întregului proces de încălzire sau de răcire, corespunzător vitezei unghiulare de rotaţie a nucleelor şi structurilor de energie momentane.

În funcţie de viteza unghiulară de rotaţie w sau de frecvenţa n, etapele proceselor de încălzire sau de răcire ale moleculelor şi atomilor sânt reprezentate pe figura 1.

Figura 1. Etapele proceselor reversibile de încălzire şi de răcire ale moleculelor şi atomilor.

 

De-a lungul tuturor etapelor proceselor reversibile de încălzire şi de răcire, moleculele emit continuu energie şi sub formă de fotoni şi în mod difuz.

Menţionăm că emisia de energie în procesele reversibile de încălzire şi de răcire ale moleculelor şi atomilor izolaţi a fost analizată şi în paragraful 11.5 „Emisia de lumină şi viteza luminii” din [1] şi este prezentată, cu aceeaşi denumire şi într-o postare pe prezentul blog.

Pentru a analiza emisia de energie în procesele termice, trebuie să determinăm diferențiala energiei moleculei, adică să determinăm creşterea funcţiei care exprimă energia moleculei raportată la tangenta la funcţie într-un punct al ei.

Conform [2] pag. 304, diferenţiala funcţiei y = f(x) se determină cu relaţia

       (44)

Aplicând relaţia (44) energiei moleculei exprimată prin relaţia (11.73) din [1], se obţine:

         (45)

Înmulțind și împărțind cu w_n în membrul doi al relației (45), se obţine

           (46)

energia moleculei E_m fiind dublul sumei energiilor nucleelor E_n și structurilor de energie E_s.

Cum E_m și w_n sânt mărimi pozitive, semnul creşterii dE_m este acelaşi cu semnul  creşterii dw_n, adică:

-        w_n = const şi dw_n = 0, rezultă că şi dE_m = 0 şi E_m = const, respectiv E_n = const și E_s = const.

-        creşte w_n şi dw_n > 0, rezultă că şi dE_m > 0 şi creşte şi E_m, respectiv cresc și E_n și E_s;

-        scade w_n şi dw_n < 0, rezultă că şi dE_m < 0 şi scade şi E_m, respectiv scad și E_n și E_s;

Aceste trei cazuri reprezintă, de fapt, cazurile regimului termic în care se poate afla molecula, în schimbul de energie cu mediul înconjurător, cu câmpul universal de energie, descrise în subparagraful 11.7.6.1 din [1] şi pe care le reproducem:

-        staţionar, E_im = E_em, adică energia care intră în moleculă este egală cu energia care iese din moleculă,

-        de încălzire, E_im > E_em, adică energia care intră în moleculă este mai mare ca energia care iese din moleculă şi

-        de răcire, E_im < E_em, adică energia care intră în moleculă este mai mică decât energia care iese din moleculă.

Aşa cum rezultă din toată analiza de mai sus, molecula, oriunde s-ar afla în câmpul universal de energie, este tot timpul conectată şi se află într-un schimb permanent de energie cu acesta, indiferent de regimul termic în care se găseşte.

 În mod natural, sub acţiunea legii atracţiei dintre energii, molecula tinde şi se stabilizează în regimul termic staţionar de valori E_m şi w_n, deoarece în acest regim, forţele de atracţie şi centrifuge din interiorul său echilibrează complet acţiunea externă a forţei de atracţie a câmpului universal de energie.

Pentru a trece molecula din regimul staţionar în regimul de încălzire, adică pentru a creşte fluxul de energie prin moleculă peste valoarea corespunzătoare regimului staţionar, forţei externe a câmpului universal de energie trebuie să i se alăture încă o forţă externă care să fie capabilă să producă creşterea fluxului de energie. Fluxul de energie prin moleculă creşte până la valoarea la care forţele de atracţie şi centrifuge din interiorul moleculei ajung să echilibreze acţiunea comună a forţelor externe, când molecula trece din nou în regim staţionar cu un surplus DE_m de energie. Creşterea forţelor de atracţie şi centrifuge din interiorul moleculei se produce pe seama creşterii vitezei unghiulare de rotaţie w_n a nucleelor atomilor moleculei cu Dw_n, corespunzătoare surplusului DE_m de energie.

După încetarea acţiunii forţei externe, rămânând ca exterioară doar forţa câmpului universal de energie, acţiunea combinată a forţelor de atracţie şi centrifuge din interiorul moleculei depăşeşte forţa externă şi regimul staţionar realizat la surplusul DE_m de energie se strică.

 Sub acţiunea forţelor de atracţie şi centrifuge din interiorul său, molecula începe să arunce mai multă energie în exterior, surplusul DE_m de energie începe să diminueze şi, corespunzător diminuează şi creşterea Dw_n a vitezei unghiulare de rotaţie w_n a nucleelor moleculei. Molecula trece într-un regim liber de răcire care continuă până la epuizarea completă a surplusului DE_m de energie şi molecula revine la regimul staţionar iniţial cu E_m şi w_n.

Trebuie să menţionăm că forţa exterioară adăugată la forţa câmpului universal de energie poate acţiona şi în sens invers celui descris mai sus. Adică, în loc să sporească energia moleculei să o micşoreze cu  (– DE_m), cum se întâmplă în instalaţiile frigorifice. În asemenea cazuri, molecula trece din regimul staţionar într-un regim de răcire. La un moment dat, şi în asemenea cazuri, la echilibrul forţelor interne cu forţele externe se instalează un regim staţionar la un deficit de – DE_m de energie şi o diminuare de – Dw_m a vitezei unghiulare de rotaţie.

La încetarea forţei exterioare care a provocat răcirea, sub acţiunea forţelor de atracţie ale energiei structurilor de energie din jurul nucleelor, care tinde către infinit în zonele polare ale găurilor lipsite de energie, începe procesul de încălzire, adică de creştere a fluxului de energie prin moleculă şi completarea deficitului ei de energie. Procesul de încălzire se încheie prin revenirea la regimul normal de stabilizare, adică atât deficitul de energie cât şi diminuarea vitezei unghiulare de rotaţie devin zero, – DE_m = 0 şi – Dw_m = 0, valori la care, forţele centrifuge ale structurilor de energie din jurul nucleelor echilibrează şi stabilizează fluxul de energie prin moleculă astfel încât energia care intră în moleculă este constantă şi egală cu energia care iese din moleculă.  

Astfel se petrec procesele termice în moleculă, indiferent de mărimea sau complexitatea ei, dar şi în oricare corp material de pe planeta noastră, din sistemul planetar, din Galaxie şi chiar din Univers. Prin înlocuirea cuvântului „moleculă” cu cuvintele „corp material”, toată analiza de mai sus este aplicabilă oricărui corp material format din molecule, deoarece proce-sele termice din corpul material constau dintr-un ansamblu de procese moleculare ce se petrec identic şi simultan, în toate moleculele corpului material.

În încheierea analizei, este necesar să facem observaţia că relaţia (46)119) aminteşte de relaţia entropiei, dacă ţinem seama de echivalenţa w_m »T^o. În înţelesul său clasic, entropia (S) este definită în [3] ca o funcţie de stare a unui sistem termodinamic exprimată prin relaţia

           (47)

pentru sisteme reversibile, şi prin relaţia

         (48)

pentru sisteme ireversibile.

Deoarece T^o > 0, dQ şi dS au întotdeauna acelaşi semn în ambele relaţii (47) şi (48). Rezultă că acumularea de căldură înseamnă creşterea entropiei, iar cedarea de căldură înseamnă scăderea entropiei sistemului.

Conform principiului al doilea al termodinamicii, sensul transformărilor termice spontane este acela că orice proces spontan tinde să treacă de la o stare mai puţin probabilă la una mai probabilă, parametrul de stare care determină sensul transformării de energie fiind entropia S. Prin urmare, orice variaţie a entropiei unui corp material înseamnă schimb de căldură (de energie) între corp şi mediul înconjurător. Dacă entropia creşte, corpul primeşte energie şi se încălzeşte, iar dacă entropia scade, corpul se răceşte.

Aşa fiind înţeles principiul entropiei în fizica contemporană, pe considerentele acestuia este clădită teoria „ordinii şi dezordinii” şi este trasă concluzia că Universul evoluează implacabil spre entropia zero, adică spre moarte şi apoi renaşterea printr-un nou bing-bang.

În fond, principiul entropiei nu numai că nu fundamentează aberaţii ca cele din alineatul precedent, ba dimpotrivă se dovedeşte a fi o consecinţă şi o confirmare a legii fundamentale a forţei de atracţie a energiei universale. Conform analizei de mai sus, principiul entropiei corespunde concepţiei elaborate în [1] şi se încadrează în analiza proceselor termice efectuată de-a lungul prezentului paragraf. 

Respingând aberaţiile fizicienilor contemporani, care nu sânt decât un pamflet umoristic, nu putem să trecem cu vederea meritele deosebite ale fizicianului  Rudolf Clausius, cel care a formult şi fundamentat principiul entropiei. Într-o epocă în care cercetarea se baza preponderent pe rezulatae obţinute în experimente întâmplătoare, Rudolf Clausius s-a ridicat deasupra lor şi a intuit şi sintetizat corect observaţiile adunate asupra fenomenelor termice, reuşind să fundamenteze un principiu care este consecinţa directă a uneia dintre legile fundamentale ale Universului. Tot respectul pentru un asemenea mare fizician.

Într-adevăr, să revenim la relaţiile lui Clausius (47) şi (48): dS = 0 înseamnă şi dQ = 0 şi, implicit, T = constant. Şi dacă o asemenea stare este extinsă la nivelul Universului, înseamnă o totală liniştire energetică la întreaga sa scară, înseamnă că pe tot cuprinsul Universului nu mai există energii diferite în două puncte diferite. Totodată, asta înseamnă şi încetarea oricărei mişcări, în întreg Universul, înseamnă echilibrarea completă a forţelor de atracţie dintre diferitele elemente de energie din întreg Universul. Dar, deşi teoretic există o asemenea posibilitate, practic ea nu se poate realiza deoarece, Universul fiind bântuit de un nesfârşit număr de mişcări giroscopice de tipul galaxiilor, care-şi perpetuează existenţa prin vânturarea unor enorme cantităţi de energie şi prin dispariţia treptată într-un loc şi apariţia treptată în alt loc, perpetuarea existenţei şi evoluţiei galaxiilor este veşnică. Aşa că Universul este şi va fi veşnic.

Aducerea în discuţie a Universului dar şi faptul că evoluţiile caracteristice etapelor extreme de pe figura 1 din postarea (I) au desfăşurări cosmice, ne determină ca de analiza acestora să ne preocupăm în postarea (III). 

Bibliografia

1  CONSTANTIN TEODORESCU: Structură şi evoluţie. Editura MATRIX ROM. Bucureşti 2016. Ediţia a 5 – a revizuită şi adăugită.

2  I. N. BRONŞTEIN, K.A. SEMENDEAEV: Spravocinik po matematike dlea injenerov i uciaşcihşia vtuzov. Izdanie desiatoe stereotipnoe. Izdatelstvo “NAUKA”. Moskva. 1964.

3  ION DIMA (coordonator): Dicţionar de fizică. Editura enciclopedică română, Bucureşti, 1972.